2023-2024学年四川省成都市双流中学高二（上）第一次月考数学试卷

一、单选题（本大题共8个小题，每小题5分，共40分）

• 1．复数

  ai

  -

  1

  i

  在复平面上对应的点位于第一象限，则实数a的取值范围是（　　）

  A．（-∞，-1）

  B．（-∞，0）

  C．（0，+∞）

  D．（1，+∞）
  组卷：260引用：4难度：0.8

  解析

• 2．某小区有500人自愿接种新冠疫苗，其中49～59岁的有140人，18～20岁的有40人，其余为符合接种条件的其他年龄段的居民．在一项接种疫苗的追踪调查中，要用分层抽样的方法从该小区18～20岁的接种疫苗的人群中抽取4人，则样本容量为（　　）

  A．14

  B．18

  C．32

  D．50
  组卷：85引用：2难度：0.8

  解析

• 3．已知P₁（1，-1，2），P₂（3，1，0），P₃（0，1，3），则向量

  P

  1

  P

  2

  与

  P

  1

  P

  3

  的夹角是（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：109引用：4难度：0.8

  解析

• 4．两平行直线3x+4y-3=0与6x+8y+1=0之间的距离为（　　）

  A． 2 5

  B． 7 10

  C． 4 5

  D． 9 10
  组卷：57引用：3难度：0.8

  解析

• 5．已知α，β为两个不同平面，m,n为两条不同直线，则下列说法不正确的是（　　）

  A．若m⊥α，n⊥α，则m∥n

  B．若m⊥α，m⊥n,则n∥α

  C．若m⊥α，m⊥β，则α∥β

  D．若m⊥α，n⊥β，且α⊥β，则m⊥n
  组卷：294引用：3难度：0.6

  解析

• 6．平面α过棱长为1的正方体ABCD-A₁B₁C₁D₁的面对角线AB₁，且α⊥平面C₁BD，α∩平面ADD₁A₁=AS，点S在直线A₁D₁上，则AS的长度为（　　）

  A． 5

  B． 2

  C． 5 2

  D．1
  组卷：23引用：2难度：0.7

  解析

• 7．已知圆C：（x-4）²+（y-2）²=r²截y轴所得的弦长为2

  2

  ，过点（0，4）且斜率为k的直线l与圆C交于A、B两点，若|AB|=2

  2

  ，则k的值为（　　）

  A．- 1 4

  B． 1 4

  C．- 3 4

  D． 3 4
  组卷：179引用：5难度：0.7

  解析

三、解答题（本大题共6个大题，共70分）

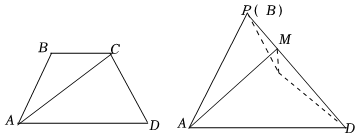• 21．如图，等腰梯形ABCD中，AD∥BC，AB=BC=CD=

  1

  2

  AD，现以AC为折痕把△ABC折起，使点B到达点P的位置，且PA⊥CD．
  （1）证明：平面APC⊥平面ADC；
  （2）若M为PD上一点，且三棱锥D-ACM的体积是三棱锥P-ACM体积的2倍，求二面角P-AC-M的余弦值．
  组卷：80引用：2难度：0.6

  解析

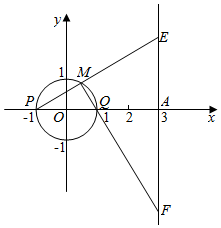• 22．已知圆O：x²+y²=1，直线l过点A（3，0）且与圆O相切．
  （Ⅰ）求直线l的方程；
  （Ⅱ）如图，圆O与x轴交于P，Q两点，点M是圆O上异于P、Q的任意一点，过点A且与x轴垂直的直线为l₁，直线PM交直线l₁于点E，直线QM交直线l₁于点F，求证：以EF为直径的圆C与x轴交于定点B，并求出点B的坐标．
  组卷：170引用：3难度：0.6

  解析