2022-2023学年上海市宝山区吴淞中学高二（下）月考数学试卷（5月份）

一、单选题

• 1．等比数列{a_n}的前n项和是S_n，且a₁=1，若

  S

  10

  S

  5

  =

  31

  32

  ，则

  S

  15

  S

  10

  =（　　）

  A． 3 2

  B． 31 32

  C． - 1 32

  D． 993 992
  组卷：259引用：5难度：0.6

  解析

• 2．如图所示，已知正方体ABCD-A₁B₁C₁D₁，E，F分别是正方形A₁B₁C₁D₁和ADD₁A₁的中心，则EF和CD所成的角是（　　）

  A．60°

  B．45°

  C．30°

  D．135°
  组卷：68引用：4难度：0.5

  解析

• 3．能够把椭圆

  x

  2

  4

  +

  y

  2

  =

  1

  的周长和面积同时分为相等的两部分的函数称为椭圆的“可分函数”，下列函数中不是椭圆的“可分函数”的为（　　）

  A．f（x）=4x3+x	B． f （ x ） = ln 5 - x 5 + x
  C．f（x）=sinx	D．f（x）=ex+e-x
  组卷：46引用：3难度：0.6

  解析

• 4．数列{a_n}中，

  a

  n

  =

  lo

  g

  n

  +

  1

  （

  n

  +

  2

  ）

  （

  n

  ∈

  N

  *

  ）

  ，定义：使a₁•a₂•…•a_k为整数的数k（k∈N^*）叫做期盼数，则区间[1，2023]内的所有期盼数的和等于（　　）

  A．2023

  B．2024

  C．2025

  D．2026
  组卷：387引用：9难度：0.5

  解析

二、填空题

• 5．已经抛物线方程y²=4x,则其准线方程为

  ．
  组卷：44引用：1难度：0.9

  解析

• 6．已知数列{a_n}的通项公式为

  a

  n

  =

  2 n , n = 1 ，

  2 - n ， n ≥ 2 ，

  前n项和为S_n，则

  lim

  n

  →

  +

  ∞

  S

  n

  =

  ．
  组卷：179引用：4难度：0.6

  解析

• 7．已知直线l的方程为

  x

  2

  +

  y

  2

  =

  1

  ，则直线l的倾斜角α=

  ．
  组卷：315引用：5难度：0.9

  解析

三、解答题

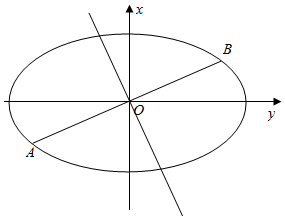• 20．在平面直角坐标系xoy中，已知椭圆C的方程为

  x

  2

  8

  +y²=1，设AB是过椭圆C中心O的任意弦，l是线段AB的垂直平分线，M是l上与O不重合的点．
  （1）求以椭圆的焦点为顶点，顶点为焦点的双曲线方程；
  （2）若MO=2OA，当点A在椭圆C上运动时，求点M的轨迹方程；
  （3）记M是l与椭圆C的交点，若直线AB的方程为y=kx（k＞0），当△AMB面积取最小值时，求直线AB的方程．
  组卷：123引用：4难度：0.3

  解析

• 21．设{a_n}是公差不为零的等差数列，满足a₁=1，a₆+a₇=a₁₃，设正项数列{b_n}的前n项和为S_n，且4S_n+2b_n=3．
  （1）求数列{a_n}和{b_n}的通项公式；
  （2）在b₁和b₂之间插入1个数x₁₁，使b₁、x₁₁、b₂成等差数列；在b₂和b₃之间插入2个数x₂₁、x₂₂，使b₂、x₂₁、x₂₂、b₃成等差数列；…；在b_n和b_n+1之间插入n个数x_n1、x_n2、…、x_nn，使b_n、x_n1、x_n2、…、x_nn、b_n+1成等差数列，求T_n=x₁₁+x₂₁+x₂₂+…+x_n1+x_n2+…+x_nn；
  （3）对于（2）中求得的T_n，是否存在正整数m、n,使得

  T

  n

  =

  a

  m

  +

  1

  2

  a

  m

  成立？若存在，求出所有的正整数对（m,n）；若不存在，请说明理由．
  组卷：228引用：4难度：0.2

  解析