2022-2023学年浙江省北斗联盟高一(下)期中数学试卷
发布:2024/5/8 8:0:8
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.设集合A={x|-1≤x≤3},B={x|0<x<4},则A∪B=( )
组卷:249引用:4难度:0.9 -
2.已知复数z=a+bi(a,b∈R)是复数
的共轭复数,则3a+b=( )21+i组卷:31引用:2难度:0.9 -
3.已知a∈R,则(a+1)(a-2)<0是0<a<1成立的( )
组卷:723引用:8难度:0.7 -
4.在△ABC中,
,记AD=3DC,BA=a,则BD=b=( )BC组卷:154引用:3难度:0.8 -
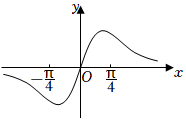 5.已知函数f(x)=ex+e-x,g(x)=sinx,则图象为如图的函数可能是( )组卷:98引用:3难度:0.7
5.已知函数f(x)=ex+e-x,g(x)=sinx,则图象为如图的函数可能是( )组卷:98引用:3难度:0.7 -
 6.由华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),其侧面三角形底边上的高与底面正方形边长的比值为,则以该四棱锥的高为边长的正方形面积与该四棱锥的侧面积之比为( )5+14组卷:444引用:6难度:0.7
6.由华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),其侧面三角形底边上的高与底面正方形边长的比值为,则以该四棱锥的高为边长的正方形面积与该四棱锥的侧面积之比为( )5+14组卷:444引用:6难度:0.7 -
7.记函数
的最小正周期为T,若f(x)=sin(ωx+π4)+b(ω>0),且y=f(x)的图象关于点2π3<T<π中心对称,则(3π2,2)=( )f(π5)组卷:133引用:1难度:0.6
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
 21.如图,为了迎接亚运会,某公园修建了三条围成一个直角三角形的观光大道AB,BC,AC,其中直角边BC=200m,斜边AB=400m,现有一个旅游团队到此旅游,甲、乙、丙三位游客分别在AB,BC,AC这三条观光大道上行走游览.
21.如图,为了迎接亚运会,某公园修建了三条围成一个直角三角形的观光大道AB,BC,AC,其中直角边BC=200m,斜边AB=400m,现有一个旅游团队到此旅游,甲、乙、丙三位游客分别在AB,BC,AC这三条观光大道上行走游览.
(1)若甲以每分钟40m的速度、乙以每分钟120m的速度都从点B出发在各自的大道上奔走,乙比甲迟2分钟出发,当乙出发1分钟后到达E,甲到达D,求此时甲、乙两人之间的距离;
(2)甲、乙、丙所在位置分别记为点D,E,F.设∠CEF=θ,乙、丙之间的距离是甲、乙之间距离的2倍,且,请将甲、乙之间的距离y表示为θ的函数,并求甲、乙之间的最小距离.∠DEF=π3组卷:33引用:3难度:0.6 -
22.已知函数f(x)=ex(x∈R),其中e为自然对数的底数,记g(x)=f(x)+f(-x).
(1)解不等式f(2x)+2f(x)≤8;
(2)若存在,使得x0∈(0,ln2]成立,求实数k的取值范围.g(2x0)=k•g2(x0)-1组卷:26引用:1难度:0.5


