当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省南京市栖霞区四校联考八年级（上）调研数学试卷（11月份）

发布：2024/9/9 22:0:8

1．某软件其中四个功能的图标如下，四个图标中是轴对称图形的是（　　）
A． B． C． D．
组卷：63引用：7难度：0.7
解析
2．在实数
22
7
，
-
3
，-3.14，0，2π，
-
3
27
中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：124引用：4难度：0.5
解析
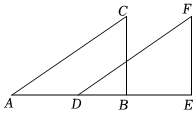3．如图，AC=DF，BC=EF，下列条件中，能证明△ABC≌△DEF的是（　　）
A．∠A=∠FDE B．CB∥FE C．∠CBA=∠FED D．AD=BE
组卷：29引用：3难度：0.5
解析
4．某礼品包装盒为体积900cm³的正方体，若这个正方体棱长为x cm,则x的范围为（　　）
A．7＜x＜8 B．8＜x＜9 C．9＜x＜10 D．10＜x＜11
组卷：85引用：5难度：0.9
解析
5．满足下列条件的△ABC不是直角三角形的是（　　）
A．∠A：∠B：∠C=3：4：5 B．BC=1，AC=2，AB=
5
C．BC：AC：AB=3：4：5 D．BC=1，AC=2，AB=
3
组卷：663引用：14难度：0.6
解析
6．如图1，在△ABC中，∠C=90°，M为AB中点．将△ACM沿CM翻折，得到△DCM（如图2），P为CD上一点，再将△DMP沿MP翻折，使得D与B重合（如图3），给出下列四个命题：①BP∥AC；②△PBC≌△PMC；③PC⊥BM；④∠BPC=∠BMC．其中真命题的是（　　）
A．①④ B．②④ C．①②③ D．①③④
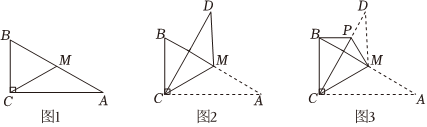组卷：85引用：2难度：0.5
解析

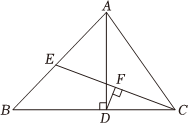22．如图，在△ABC中，AD是BC边上的高，CE是AB边上的中线，DF⊥CE于F，CD=AE．
（1）求证：CF=EF；
（2）若CE⊥AB，求∠BAD的度数．
组卷：84引用：2难度：0.5
解析
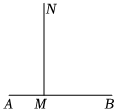23．如图，射线MN⊥AB，点C从M出发，沿射线MN运动，AM=1，MB=4．
（1）当点C运动到MC=4时，且BD⊥AC，求MD的长；
（2）当△ABC为等腰三角形时，求MC的长；
（3）经研究发现点C在运动的过程中，若△ABC的形状也发生变化，请直接写出△ABC为锐角、直角、钝角三角形时MC的对应长度取值范围．
组卷：84引用：2难度：0.6
解析