2022-2023学年新疆乌鲁木齐六十六中九年级（上）期中数学试卷

一、单选题（每小题5分，共45分）

• 1．下列方程中是一元二次方程的是（　　）

  A．x2-2xy-1=0

  B．2x- 1 x +1=0

  C．x2+ax+b=0

  D．2 x -3=0
  组卷：6引用：2难度：0.5

  解析

• 2．用配方法解方程x²+6x-1=0时，配方变形结果正确的是（　　）

  A．（x+3）2=8

  B．（x-3）2=8

  C．（x+3）2=10

  D．（x-3）2=10
  组卷：40引用：6难度：0.7

  解析

• 3．某航空公司有若干飞机场，每两个飞机场之间都开辟一条航线，一共开辟了45条航线，则这个航空公司共有飞机场（　　）

  A．8个

  B．9个

  C．10个

  D．11个
  组卷：50引用：2难度：0.7

  解析

• 4．在下列命题中，正确的是（　　）

  A．长度相等的两条弧是等弧

  B．相等的圆心角所对的弧相等

  C．相等的弧所对的弦相等

  D．圆周角的度数等于圆心角度数的一半
  组卷：109引用：4难度：0.6

  解析

• 5．某校准备修建一个面积为300平方米的矩形活动场地，它的长比宽多12米，设场地的宽为x米，根据题意可列方程为（　　）

  A．x（x-12）=300	B．2x+（x+12）=300
  C．x（x+12）=300	D．2x+2（x+12）=300
  组卷：6引用：3难度：0.6

  解析

• 6．函数y=ax²+ax+a（a≠0）的图象可能是下列图象中的（　　）

  A．

  B．

  C．

  D．
  组卷：1994引用：8难度：0.7

  解析

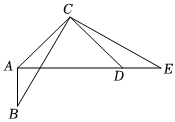• 7．如图，在△ABC中，∠BAC=135°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，下列结论不正确的是（　　）

  A．△ABC≌△DEC

  B．∠ADC=45°

  C．AD= 2 AC

  D．AE=AB+CD
  组卷：1320引用：17难度：0.6

  解析

三、解答题（共75分）

• 22．如图，Rt△ABC中，∠ABC=90°，点O，D分别在AB，AC上，CD=CB，⊙O经过点B，D，弦DF⊥AB于点E，连接BF．
  （1）求证：AC为⊙O的切线；
  （2）若∠A=30°，AE=3，求DF的长．
  组卷：13引用：2难度：0.5

  解析

• 23．在平面直角坐标系中，抛物线y=ax²+2ax-3a（a≠0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，该抛物线的顶点为D．
  （1）求该抛物线的对称轴及点A、B的坐标；
  （2）当a＞0时，如图1，连接AD，BD，是否存在实数a,使△ABD为等边三角形？若存在求出实数a的值若不存在，请说明理由；
  （3）当a=1时，如图2，点P是该抛物线上一动点，且位于第三象限，连接AP，直线PO交AC于点Q，△APQ和△OCQ的面积分别为S₁和S₂，当S₁-S₂的值最大时求直线PO的解析式．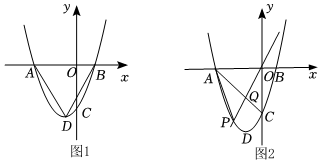
  
  组卷：504引用：4难度：0.2

  解析