2021-2022学年广东省佛山二中高二（上）期中数学试卷

一、单选题：本题共8小题，每小题5分，共40分，

• 1．已知袋中有大小、形状完全相同的5张红色、2张蓝色卡片，从中任取3张卡片，则下列判断不正确的是（　　）

  A．事件“都是红色卡片”是随机事件

  B．事件“都是蓝色卡片”是不可能事件

  C．事件“至少有一张蓝色卡片”是必然事件

  D．事件“有1张红色卡片和2张蓝色卡片”是随机事件
  组卷：944引用：5难度：0.8

  解析

• 2．已知直线l的方向向量为（1，2，3），平面α的法向量为（2，m,6），若l∥α，则m=（　　）

  A．-10

  B．3

  C．4

  D．5
  组卷：10引用：1难度：0.9

  解析

• 3．从甲袋中摸出一个红球的概率是

  1

  3

  ，从乙袋中摸出一个红球的概率是

  1

  2

  ，从两袋各摸出一个球，则2个球中恰有1个红球的概率是（　　）

  A． 5 6

  B． 1 2

  C． 2 3

  D． 1 6
  组卷：558引用：3难度：0.8

  解析

• 4．已知两条直线l₁：x+m²y+6=0，l₂：（m-2）x+3my+2m=0，若l₁与l₂平行，则m=（　　）

  A．-1或0

  B．-1

  C．0

  D．-1或0或3
  组卷：80引用：4难度：0.6

  解析

• 5．已知

  AB

  =（2，-1，3），

  AC

  =（-1，4，-2），

  AD

  =（5，-6，λ），若A，B，C，D四点共面，则实数λ为（　　）

  A．5

  B．6

  C．7

  D．8
  组卷：687引用：11难度：0.7

  解析

• 6．一束光线从A（1，0）点处射到y轴上一点B（0，2）后被y轴反射，则反射光线所在直线的方程是（　　）

  A．x+2y-2=0

  B．2x-y+2=0

  C．x-2y+2=0

  D．2x+y-2=0
  组卷：248引用：12难度：0.9

  解析

• 7．长方体ABCD-A₁B₁C₁D₁中，AB=BC=a,AA₁=2a,则D₁到直线AC的距离为（　　）

  A． 3 a

  B． 3 a 2

  C． 2 2 a 3

  D． 3 2 a 2
  组卷：20引用：3难度：0.6

  解析

四、解答题：本题共6小题，共70分解答应写出文字说明、证明过程或演算步骤.

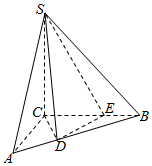• 21．如图，在三棱锥S-ABC中，SC⊥平面ABC，SC=3，AC⊥BC，CE=2EB=2，AC=

  3

  2

  ，CD=ED．
  （Ⅰ）求证：DE⊥平面SCD；
  （Ⅱ）求二面角A-SD-C的余弦值；
  （Ⅲ）求点A到平面SCD的距离．
  组卷：691引用：11难度：0.1

  解析

• 22．已知平面直角坐标系上一动点P（x,y）到点A（-2，0）的距离是点P到点B（1，0）的距离的2倍．
  （Ⅰ）求点P的轨迹方程：
  （Ⅱ）若点P与点Q关于点（-1，4）对称，求P、Q两点间距离的最大值；
  （Ⅲ）若过点A的直线l与点P的轨迹C相交于E、F两点，M（2，0），则是否存在直线l,使S_△EFM取得最大值，若存在，求出此时l的方程，若不存在，请说明理由．
  组卷：170引用：8难度：0.5

  解析