2020-2021学年浙江省丽水市庆元二中七年级(下)期中数学试卷
发布:2024/6/22 8:0:10
一、选择题(本题有10小题,每小题3分,共30分.请选出一个符合题意的正确选项,不选、多选、错选,均不给分)
-
1.计算(a2)3的结果是( )
组卷:532引用:154难度:0.9 -
2.随着微电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.0000007(平方毫米),这个数用科学记数法表示为( )
组卷:479引用:76难度:0.9 -
3.若
是方程3x+ay=1的一个解,则a的值是( )x=-1y=2组卷:1933引用:33难度:0.9 -
4.下列运算正确的是( )
组卷:187引用:4难度:0.8 -
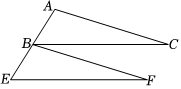 5.如图所示,△BEF是由△ABC平移所得,点A、B、E在同一直线上,若∠F=20°,∠E=68°,则∠CBF是( )组卷:7引用:1难度:0.6
5.如图所示,△BEF是由△ABC平移所得,点A、B、E在同一直线上,若∠F=20°,∠E=68°,则∠CBF是( )组卷:7引用:1难度:0.6 -
6.如果(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
组卷:22640引用:211难度:0.7 -
7.已知x2-4x-1=0,则代数式x(x-4)+1的值为( )
组卷:2336引用:19难度:0.9 -
8.若关于x,y的二元一次方程组
的解也是二元一次方程2x+3y=6的解,则k的值为( )x+y=5kx-y=9k组卷:2552引用:20难度:0.6
三、解答题(共8小题,52分)
-
23.如图1,AB,BC被直线AC所截,点D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E=70°.
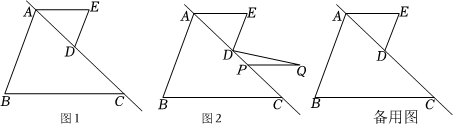
(1)AE与BC平行吗?并说明理由.
(2)将线段AE沿着直线AC平移得到线段PQ,连接DQ.①如图2,当DE⊥DQ时,求∠Q的度数;②在整个运动中,当∠Q=2∠EDQ时,求∠Q的度数.组卷:27引用:1难度:0.5 -
24.已知D是△ABC的AB边上一点,连接CD,此时有结论
,请解答下列问题:S△ACDS△BCD=ADBD
(1)当D是AB边上的中点时,△ACD的面积 △BCD的面积(填“>”“<”或“=”).
(2)如图1,点D、E分别为AB,AC边上的点,连接CD,BE交于点O,若△BOD、△COE、△BOC的面积分别为5,8,10,则△ADE的面积是 (直接写出结论).
(3)如图2,若点D,E分别是△ABC的AB,AC边上的中点,且S△ABC=60,求四边形ADOE的面积.可以用如下方法:连接AO,由AD=DB得S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△BDO=x,S△CEO=y,则S△ADO=x,S△AEO=y,由题意得S△ABE==30,S△ADC=12S△ABC=30,可列方程组为:12S△ABC,解得x+y=20,可得四边形ADOE的面积为20.解答下面问题:2x+y=30x+2y=30
如图3,D,F是AB的三等分点,E,G是CA的三等分点,CD与BE交于O,且S△ABC=60,请计算四边形ADOE的面积,并说明理由.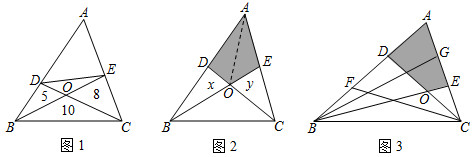 组卷:498引用:3难度:0.4
组卷:498引用:3难度:0.4


