2022-2023学年新疆喀什地区疏附县高二（上）期中数学试卷

一、单项选择题（本题共8小题，40分）

• 1．双曲线

  x

  2

  3

  -

  y

  2

  2

  =

  1

  的焦距为（　　）

  A． 3 2

  B． 5

  C． 2 5

  D． 4 5
  组卷：96引用：7难度：0.9

  解析

• 2．设两条直线的方程分别为x+y-a=0、x+y+b=0，已知a、b是关于x的方程x²+x+c=0的两个实数根，则这两条直线之间的距离是（　　）

  A． 2 4

  B． 2

  C． 2 2

  D．无法确定
  组卷：141引用：3难度：0.7

  解析

• 3．已知

  a

  、

  b

  均为单位向量，它们的夹角为60°，那么|

  a

  +

  3

  b

  |=（　　）

  A． 7

  B． 10

  C． 13

  D．4
  组卷：1507引用：137难度：0.9

  解析

• 4．直线3x+4y+12=0与圆（x-1）²+（y+1）²=9的位置关系是（　　）

  A．相交且过圆心	B．相切
  C．相离	D．相交但不过圆心
  组卷：888引用：17难度：0.9

  解析

• 5．已知抛物线E：x²=8y上一点T到E的焦点的距离为8，则点T在第一象限的横坐标是（　　）

  A．8

  B． 4 3

  C．6

  D． 4 2
  组卷：100引用：3难度：0.8

  解析

• 6．已知空间四面体D-ABC-的每条棱长都等于1，点E是AB的中点，则

  EC

  •

  DA

  等于（　　）

  A． 1 4

  B．- 1 4

  C． 3 4

  D．- 3 4
  组卷：10引用：2难度：0.9

  解析

• 7．已知中心在坐标原点的椭圆与双曲线有公共焦点，且左、右焦点分别为F₁F₂，这两条曲线在第一象限的交点为P，△PF₁F₂是以PF₁为底边的等腰三角形．若|PF₁|=10，记椭圆与双曲线的离心率分别为e₁，e₂，则e₁•e₂的取值范围是（　　）

  A．（ 1 3 ，+∞）

  B．（ 1 5 ，+∞）

  C．（ 1 9 ，+∞）

  D．（0，+∞）
  组卷：520引用：19难度：0.7

  解析

四、解答题（本题共6小题，70分）

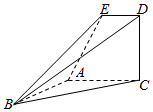• 21．已知直角梯形ACDE所在的平面垂直于平面ABC，∠BAC=∠ACD=90°，∠EAC=60°，AB=AC=AE．
  （1）若P是BC的中点，求证：DP∥平面EAB；
  （2）求平面EBD与平面ACDE所成的锐二面角θ的余弦值．
  组卷：8引用：3难度：0.5

  解析

• 22．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦点F（4，0）到渐近线的距离为

  2

  3

  ．
  （1）求双曲线C的方程；
  （2）过点F的直线与双曲线C的右支交于A，B两点，在x轴上是否存在点P，使得点F到直线PA，PB的距离相等？若存在，求出点P的坐标；若不存在，请说明理由．
  组卷：294引用：12难度：0.6

  解析