当前位置：试卷中心 > 试卷详情

2022-2023学年新疆乌鲁木齐市八一中学高二（上）第一次月考数学试卷

发布：2024/8/18 8:0:2

一、单选题

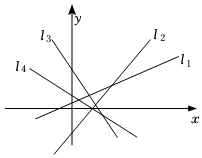1．如图，设直线l₁，l₂，l₃，l₄的斜率分别为k₁，k₂，k₃，k₄，则用“＜”号将它们的斜率k₁，k₂，k₃，k₄连接起来后，得到的结果为（　　）
A．k₁＜k₂＜k₃＜k₄ B．k₂＜k₁＜k₃＜k₄
C．k₄＜k₃＜k₁＜k₂ D．k₃＜k₄＜k₁＜k₂
组卷：225引用：4难度：0.7
解析
2．经过抛物线y²=2x的焦点且平行于直线3x-2y+5=0的直线的方程是（　　）
A．6x-4y-3=0 B．3x-2y-3=0 C．2x+3y-2=0 D．2x+3y-1=0
组卷：331引用：12难度：0.9
解析
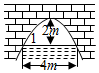3．如图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米，水位下降1米后，水面宽（　　）米．
A．
2
5
B．
2
6
C．
3
2
D．
2
3
组卷：94引用：3难度：0.7
解析
4．直线ax+y-a=0（a∈R）与圆（x-2）²+y²=4的位置关系是（　　）
A．相离 B．相交 C．相切 D．无法确定
组卷：116引用：8难度：0.7
解析
5．椭圆E：
x
2
a
2
+
y
2
a
+
2
=
1
的左、右焦点分别为F₁，F₂，过点F₁的直线l与E交于A，B两点，若△ABF₂的周长为12，则E的离心率为（　　）
A．
2
3
B．
1
3
C．
1
9
D．
4
9
组卷：252引用：2难度：0.7
解析
6．已知直线x-y+λ=0与圆O：x²+y²-6x-2y+1=0交于A，B两点，且OA⊥OB，则实数λ的值为（　　）
A．-1或-3 B．1或-5 C．3或-7 D．7或-12
组卷：43引用：4难度：0.7
解析
7．已知圆x²+y²+4x-2y+a=0上仅有一点到直线3x-4y-5=0的距离为1，则实数a的值为（　　）
A．11 B．-4 C．1 D．4
组卷：7引用：1难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题

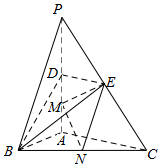21．如图，在三棱锥P-ABC中，PA⊥底面ABC，
∠
BAC
=
π
2
．点D、E、N分别为棱PA、PC、BC的中点，M是线段AD的中点，PA=AC=4，AB=2．
（1）求证：MN∥平面BDE；
（2）求二面角C-EM-N的正弦值；
（3）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为
7
7
，求线段AH的长．
组卷：188引用：7难度：0.5
解析
22．设抛物线C：y²=2px（p＞0）的焦点为F，点M在抛物线C上，O为坐标原点，已知|OM|=2
3
，|MF|=3．
（1）求抛物线C的方程；
（2）过焦点F作直线l交C于A，B两点，P为C上异于A，B的任意一点，直线PA，PB分别与C的准线相交于D，E两点，证明：以线段DE为直径的圆经过x轴上的两个定点．
组卷：209引用：5难度：0.5
解析