2022-2023学年黑龙江省齐齐哈尔市部分地区校高三(上)期中数学试卷
发布:2024/8/10 0:21:48
一、单选题:(每题5分,满分40分)
-
1.已知集合A={x|x2+x-2<0},B={x|log2x≤0},则A∩B=( )
组卷:17引用:2难度:0.8 -
2.已知z=i+i2+i3+⋯+i2022,则|z|=( )
组卷:4引用:2难度:0.8 -
3.若两个正实数x、y满足x+y=4,且不等式
-3m+5恒成立,则实数m的取值范围为( )4x+16y>m2组卷:30引用:6难度:0.7 -
4.在数列{an}中,a1=3,an=2an-1-n+2(n≥2,n∈N+),若an>980,则n的最小值是( )
组卷:26引用:4难度:0.7 -
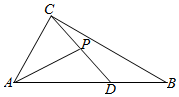 5.如图,在△ABC中,∠BAC=,π3,P为CD上一点,且满足AD=2DB=mAP+AC,若|12AB|=2,|AC|=3,则|AB|的值为( )AP组卷:209引用:5难度:0.7
5.如图,在△ABC中,∠BAC=,π3,P为CD上一点,且满足AD=2DB=mAP+AC,若|12AB|=2,|AC|=3,则|AB|的值为( )AP组卷:209引用:5难度:0.7 -
6.函数f(x)是定义在区间(0,+∞)上的可导函数,其导函数为f′(x),且满足xf′(x)+2f(x)>0,则不等式
的解集为( )(x+2016)f(x+2016)5<5f(5)x+2016组卷:397引用:6难度:0.7 -
7.已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(x+2)=-
,且当x∈[-2,0]时,f(x)=(1f(x))x-1,若在区间内方程f(x)-loga(x+2)=0(a>1)有三个不同的实数根,则实数a的取值范围为( )12组卷:113引用:5难度:0.5
四、解答题:(满分70分)
-
21.已知在平面直角坐标系中,O为坐标原点,动点M(x,y)满足
.(x+1)2+y2+(x-1)2+y2=4
(1)求动点M的轨迹C的方程;
(2)过点N(1,0)且垂直于x轴的直线l与轨迹C交于点P(P在第一象限),以P为圆心的圆与x轴交于A,B两点,直线PA,PB与轨迹C分别交于另一点S,Q,求证:直线SQ的斜率为定值,并求出这个定值.组卷:14引用:2难度:0.5 -
22.已知函数
f(x)=xex+12ax2+ax(a∈R)
(1)讨论f(x)的单调性;
(2)若关于x的不等式在(0,+∞)上恒成立,求实数a的取值范围.f(x)≥12ax2+4ax+lnx+1组卷:13引用:2难度:0.6


