2023-2024学年广东省东莞外国语学校高三(上)第二次月考数学试卷(11月份)
发布:2024/9/30 6:0:3
一、单选题(选对得5分,选错得0分.)
-
1.设集合A={x|(x+2)(x-4)<0},B={2,3,4,5},则A∩B=( )
组卷:26引用:6难度:0.8 -
2.已知c=0.20.3,b=20.2,a=log20.2,则a,b,c的大小关系为( )
组卷:158引用:2难度:0.7 -
3.函数f(x)=2x+log2x的零点所在区间是( )
组卷:222引用:10难度:0.7 -
4.已知函数f(x)=x2,g(x)=2x-2-x,如图是下列四个函数中某个函数的大致图象,则该函数是( )
 组卷:56引用:5难度:0.7
组卷:56引用:5难度:0.7 -
5.某企业不断自主创新提升技术水平,积极调整企业旗下的甲、乙、丙、丁、戊等5种系列产品的结构比例,近年来取得了显著效果.据悉该企业2022年5种系列产品年总收入是2020年的2倍,其中5种系列产品的年收入构成比例如图所示.则下列说法错误的是( )
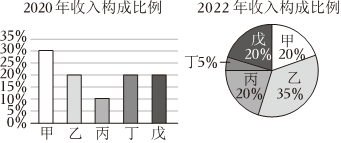 组卷:43引用:5难度:0.7
组卷:43引用:5难度:0.7 -
6.已知(ax+1)(2x-1)6展开式中x5的系数为48,则实数a=( )
组卷:721引用:4难度:0.7 -
7.设函数y=f(x)的图象与y=2x+a的图象关于y=-x对称,且f(-2)+f(-4)=1,则a=( )
组卷:6441引用:44难度:0.6
四、解答题
-
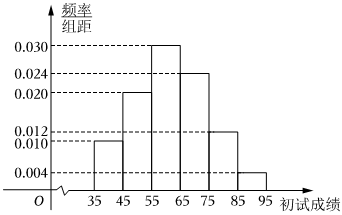 21.某校数学组老师为了解学生数学学科核心素养整体发展水平,组织本校8000名学生进行针对性检测(检测分为初试和复试),并随机抽取了100名学生的初试成绩,绘制了频率分布直方图,如图所示.
21.某校数学组老师为了解学生数学学科核心素养整体发展水平,组织本校8000名学生进行针对性检测(检测分为初试和复试),并随机抽取了100名学生的初试成绩,绘制了频率分布直方图,如图所示.
(1)根据频率分布直方图,求样本平均数的估计值;
(2)若所有学生的初试成绩X近似服从正态分布N(μ,σ2),其中μ为样本平均数的估计值,σ≈14.初试成绩不低于90分的学生才能参加复试,试估计能参加复试的人数;
(3)复试共三道题,规定:全部答对获得一等奖;答对两道题获得二等奖;答对一道题获得三等奖;全部答错不获奖.已知某学生进入了复试,他在复试中前两道题答对的概率均为a,第三道题答对的概率为b.若他获得一等奖的概率为,设他获得二等奖的概率为P,求P的最小值.18
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ<X≤μ+σ)≈0.6827,P(μ-2σ<X≤μ+2σ)≈0.9545,P(μ-3σ<X≤μ+3σ)≈0.9973.组卷:701引用:12难度:0.6 -
22.已知函数f(x)=sinx-ln(1+x),f′(x)为f(x)的导数.证明:
(1)f′(x)在区间(-1,)存在唯一极大值点;π2
(2)f(x)有且仅有2个零点.组卷:11605引用:12难度:0.2


