2022-2023学年山东省枣庄市薛城区七年级（下）期中数学试卷

一、选择题：下面每小题给出的四个选项中，只有一项是正确的，请把正确选项选出来．每小题3分，共30分．

• 1．下列运算中，计算结果正确的是（　　）

  A．a•a3=a3	B．（a2）3=a5
  C．（-a2b）2=a4b2	D．a3÷a=a3
  组卷：96引用：3难度：0.7

  解析

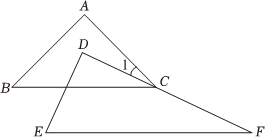• 2．一副三角板如图所示放置，斜边平行，即BC∥EF，则∠1的度数为（　　）

  A．10°

  B．15°

  C．20°

  D．30°
  组卷：88引用：2难度：0.5

  解析

• 3．从前，一位农场主把一块边长为a米（a＞4）的正方形土地租给租户张老汉，第二年，他对张老汉说：“我把这块地的一边增加4米，相邻的另一边减少4米，变成长方形土地继续租给你，租金不变，你也没有吃亏，你看如何？”如果这样，你觉得张老汉的租地面积会（　　）

  A．没有变化

  B．变大了

  C．变小了

  D．无法确定
  组卷：1561引用：5难度：0.5

  解析

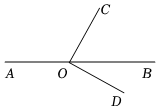• 4．如图，点O在直线AB上，OC⊥OD，若∠BOD=26°，则∠AOC的大小为（　　）

  A．116°

  B．124°

  C．126°

  D．154°
  组卷：308引用：4难度：0.7

  解析

• 5．笔记本每本a元，买3本笔记本共支出y元，下列选项判断正确的有（　　）

  A．a是常量时，y是变量

  B．a是变量时，y是常量

  C．a是变量时，y也是变量

  D．无论a是常量还是变量，y都是变量
  组卷：1040引用：5难度：0.8

  解析

• 6．已知一个水分子的直径约为4×10^-10米，某花粉的直径约为5×10^-4米，用科学记数法表示这种花粉的直径是一个水分子直径的（　　）

  A．8×10-7倍

  B．1.25×107倍

  C．8×10-6倍

  D．1.25×106倍
  组卷：248引用：3难度：0.5

  解析

• 7．心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（分钟）之间有如下关系（其中x介于0∼20之间）：
  

  提出概念所用时间	2	5	7	10	12	13	14	17	20
  对概念的接受能力	47.8	53.5	56.3	59	59.8	59.9	59.8	58.3	55

  下列说法正确的是（　　）

  A．学生对概念的接受能力是 59.8 时，提出概念所用的时间是 12 分钟

  B．在这个变化中，自变量是提出概念所用的时间，因变量是对概念的接受能力

  C．根据表格中的数据，提出概念所用的时间是 13 分钟时，学生对概念的接受能力最强

  D．根据表格中数据可知：当 x 介于 2∼13 之间时，y 值逐渐增大，学生对概念的接受能力逐步增强
  组卷：156引用：5难度：0.8

  解析

• 8．如果2（5-a）（6+a）=100，那么a²+a+1的值为（　　）

  A．19

  B．-19

  C．69

  D．-69
  组卷：2889引用：5难度：0.5

  解析

三、解答题（本题共8道大题，共72分）

• 23．综合与实践
  某数学兴趣小组的小林和小颖两位同学将连续的正整数1，2，3，…排成如图1所示的数表，从中框出某些数，做了如下探索：
  （1）小林在数表中框出“H”字形，并将相对的两数相乘，再作差，请你帮忙完成研究过程．
  ①计算：13×29-11×31=

  ，35×51-33×53=

  ．
  ②化简：图2是从图1中取出的一部分，在选中的七个数中，若设中心数为x,则a,b,c,d所对应的数分别为

  ，

  ，

  ，

  （用含x的代数式表示），请你利用整式的运算，对bc-ad进行化简．
  （2）小颖在数表中框出“T”字形，并将顶端左右两数相乘，再与底端数平方作差，即图3中mn-y²，则在框出的“T”字形中，mn-y²的值能否等于-649？若能，请求出m的值；若不能，请说明理由．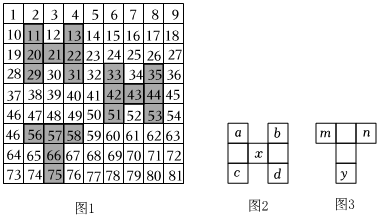
  
  组卷：296引用：4难度：0.5

  解析

• 24．如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．
  （1）求∠CBD的度数；
  （2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．
  （3）当点P运动到使∠ACB=∠ABD时，∠ABC的度数是

  ．
  组卷：8320引用：23难度：0.1

  解析