当前位置：试卷中心 > 试卷详情

2022-2023学年北京市通州区运河中学高二（上）月考数学试卷（10月份）

发布：2024/9/20 10:0:8

1．在长方体ABCD-A₁B₁C₁D₁中，
BA
+
BC
+
D
D
1
=（　　）
A．
D
1
B
1
B．
D
1
B
C．
D
B
1
D．
B
D
1
组卷：800引用：12难度：0.7
解析
2．已知向量
a
=（2，-3，1），
b
=（2，0，3），则
a
•（
a
+
b
）=（　　）
A．21 B．-21 C．20 D．-20
组卷：544引用：3难度：0.9
解析
3．若向量
a
=（1，2，0），
b
=（-2，0，1），则（　　）
A．cos＜
a
，
b
＞=-
2
5
B．
a
⊥
b
C．
a
∥
b
D．|
a
|=|
b
|
组卷：303引用：14难度：0.9
解析
4．已知空间向量
a
=（2，1，-1），
b
=（x,-2，2），且
a
∥
b
，则x=（　　）
A．-2 B．-4 C．2 D．4
组卷：46引用：4难度：0.8
解析
5．已知直线l₁，l₂的方向向量分别为
a
=（1，2，-2），
b
=（-2，1，m），若l₁⊥l₂，则m等于（　　）
A．1 B．2 C．0 D．3
组卷：125引用：3难度：0.8
解析
6．已知M为z轴上一点，且点M到点A（-1，0，1）与点（1，-3，2）的距离相等，则点M的坐标为（　　）
A．（3，0，0） B．（0，-2，0） C．（0，0，6） D．（0，0，-3）
组卷：554引用：2难度：0.8
解析
7．已知{
a
，
b
，
c
}是空间向量的一个基底，则下列向量中能与
a
+
b
，
a
-
b
构成基底的是（　　）
A．
a
B．
b
C．
c
D．
a
+2
b
组卷：46引用：4难度：0.8
解析

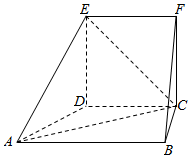22．在如图所示的几何体中，四边形CDEF为正方形，四边形ABCD为直角梯形，AB∥CD，BC⊥CD，BC⊥CF，AB=3BC=3CD．
（1）求BE与平面EAC所成角的正弦值；
（2）线段ED或其延长线上是否存在点P，使平面EAC⊥平面PBC？证明你的结论．
组卷：67引用：4难度：0.6
解析
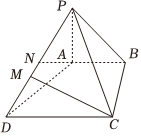23．如图，在四棱锥P-ABCD中，PA⊥面ABCD，AB∥CD，且CD=2，AB=1，
BC
=
2
2
，PA=1，AB⊥BC，N为PD的中点．
（Ⅰ）求直线AN到平面PBC的距离；
（Ⅱ）在线段PD上是否存在一点M，使得直线CM与平面PBC所成角的正弦值是
1
3
，若存在，求出
DM
DP
的值，若不存在，说明理由．
组卷：14引用：1难度：0.5
解析