2022-2023学年浙江省宁波市余姚市兰江中学八年级（上）期中数学试卷

一.选择题（共10小题，满分30分，每小题3分）

• 1．三角形是指（　　）

  A．由三条线段所组成的封闭图形

  B．由不在同一直线上的三条直线首尾顺次相接组成的图形

  C．由不在同一直线上的三条线段首尾顺次相接组成的图形

  D．由三条线段首尾顺次相接组成的图形
  组卷：1467引用：7难度：0.7

  解析

• 2．下列数值是不等式x＜2的解的是（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：298引用：5难度：0.8

  解析

• 3．下列各组长度的三条线段能组成三角形的是（　　）

  A．1，2，3

  B．1，1，2

  C．2，2，3

  D．1，3，7
  组卷：277引用：8难度：0.7

  解析

• 4．下列对△ABC的判断，错误的是（　　）

  A．若∠A：∠B：∠C=1：2：3，则△ABC是直角三角形

  B．若∠A=30°，∠B=50°，则△ABC是锐角三角形

  C．若AB=AC，∠B=40°，则△ABC是钝角三角形

  D．若2∠A=2∠B=∠C，则△ABC是等腰直角三角形
  组卷：2297引用：14难度：0.6

  解析

• 5．下列生活实例中，利用了“三角形稳定性”的是（　　）

  A．

  B．

  C．

  D．
  组卷：1000引用：13难度：0.7

  解析

• 6．若等腰三角形的两边长分别为2和5，则它的周长为（　　）

  A．9

  B．7

  C．12

  D．9或12
  组卷：5147引用：49难度：0.9

  解析

• 7．如果将一副三角板按如图的方式叠放，则∠1的度数为（　　）

  A．105°

  B．120°

  C．75°

  D．45°
  组卷：1668引用：16难度：0.7

  解析

• 8．定义新运算“⊕”如下：当a＞b时，a⊕b=ab+b；当a＜b时，a⊕b=ab-b,若3⊕（x+2）＞0，则x的取值范围是（　　）

  A．-1＜x＜1或x＜-2	B．x＜-2或1＜x＜2
  C．-2＜x＜1或x＞1	D．x＜-2或x＞2
  组卷：1318引用：10难度：0.6

  解析

三.解答题（共8小题，满分66分）

• 23．某数学兴趣小组开展了一次活动，过程如下：设∠BAC=θ（0°＜θ＜90°）．现把小棒依次摆放在两射线之间，并使小棒两端分别落在射线AB、AC上．
  
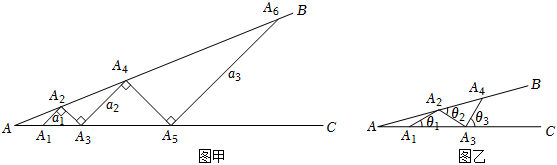
  活动一：
  如图甲所示，从点A₁开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直，A₁A₂为第1根小棒．
  数学思考：（1）小棒能无限摆下去吗？答：

  ．（填“能”或“不能”）
  （2）设AA₁=A₁A₂=A₂A₃，θ=

  ；
  活动二：
  如图乙所示，从点A₁开始，用等长的小棒依次向右摆放，其中A₁A₂为第1根小棒，且A₁A₂=AA₁．
  数学思考：（3）若已经摆放了3根小棒，θ₃=

  ；（用含θ的式子表示）
  （4）若只能摆放5根小棒，求θ的范围．
  组卷：1041引用：6难度：0.6

  解析

• 24．【发现问题】小强在一次学习过程中遇到了下面的问题：如图①，AD是△ABC的中线，若AB=5，AC=3，求AD的取值范围．
  
  【探究方法】小强所在的小组通过探究发现，延长AD至点E．使ED=AD．连接BE．
  可以证出△ADC≌△EDB，利用全等三角形的性质可将已知的边长与AD转化到△ABE中，进而求出AD的取值范围．
  方法小结：从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．
  （1）请你利用上面解答问题的思路方法，写出求AD的取值范围的过程；
  【问题解决】
  （2）如图②，CB是△AEC的中线，CD是△ABC的中线，且AB=AC，下列四个选项中：
  A．∠ACD=∠BCD
  B．CE=2CD
  C．∠BCD=∠BCE
  D．CD=CB
  直接写出所有正确选项的序号是

  ．
  【问题拓展】
  （3）如图③，在△ABO和△CDO中，OA=OB，OC=OD，∠AOB与∠COD互补，连接AC、BD，E是BD的中点，求证：OE=

  1

  2

  AC．
  组卷：488引用：2难度：0.3

  解析