当前位置：试卷中心 > 试卷详情

2022-2023学年河北省唐山市曹妃甸一中高二（下）期末数学试卷

发布：2024/5/21 8:0:9

一、单选题（本题共8小题，每小题5分，共40分）

1．（x²+
3
x
）⁵的展开式中x⁴的系数是（　　）
A．90 B．80 C．70 D．60
组卷：399引用：14难度：0.7
解析
2．已知函数f（x）的导函数为f′（x），且满足f（x）=2xf′（1）+lnx,则f′（2）=（　　）
A．
3
2
B．1 C．-1 D．-
3
2
组卷：408引用：15难度：0.9
解析
3．某市一次高三模拟考试一共有3.2万名考生参加，他们的总分ξ服从正态分布N（480，σ²），若P（430≤ξ≤530）=0.78，则总分高于530分的考生人数为（　　）
A．2400 B．3520 C．8520 D．12480
组卷：311引用：7难度：0.8
解析
4．5名学生参加数学建模活动，目前有3个不同的数学建模小组，每个小组至少分配1名学生，至多分配3名学生，则不同的分配方法种数为（　　）
A．60 B．90 C．150 D．240
组卷：80引用：3难度：0.8
解析
5．（1+x）³+（1+x）⁴+⋯+（1+x）⁹的展开式中x³的系数是（　　）
A．84 B．120 C．122 D．210
组卷：238引用：4难度：0.7
解析
6．已知
C
0
n
+
2
C
1
n
+
2
2
C
2
n
+
2
3
C
3
n
+
⋯
+
2
n
C
n
n
=
81
，则
C
1
n
+
C
2
n
+
C
3
n
+
⋯
+
C
n
n
等于（　　）
A．15 B．16 C．7 D．8
组卷：423引用：6难度：0.8
解析
7．我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果，功不可没．三药”分别为金花清感颗粒、连花清瘟胶囊、血必清注射液；“三方”分别为清肺排毒汤、化湿败毒方、宣肺败毒方．若某医生从“三药三方”中随机选出两种，事件A表示选出的两种中至少有一药，事件B表示选出的两种中有一方，则P（B|A）=（　　）
A．
1
5
B．
3
10
C．
3
5
D．
3
4
组卷：927引用：18难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共6小题，17题10分，其余每题12分，共70分，解答应写出文字说明、证明过程或演算步骤）

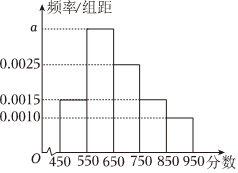21．某学校共有1000名学生参加知识竞赛，其中男生400人，为了解该校学生在知识竞赛中的情况，采用分层随机抽样的方法抽取了100名学生进行调查，分数分布在450～950分之间，根据调查的结果绘制的学生分数频率分布直方图如图所示．将分数不低于750分的学生称为“高分选手”．
（1）求a的值；
（2）现采用分层随机抽样的方式从分数落在[550，650）、[750，850）内的两组学生中抽取10人，再从这10人中随机抽取3人，记被抽取的3名学生中属于“高分选手”的学生人数为随机变量X，求X的分布列及数学期望；
（3）若样本中属于“高分选手”的女生有10人，试完成下列2×2列联表，依据α=0.025的独立性检验，能否认为该校学生属于“高分选手”与“性别”有关联？

属于“高分选手” 不属于“高分选手” 合计

男生

女生

合计

（参考公式：
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，其中n=a+b+c+d）

α 0.150 0.100 0.050 0.025 0.010 0.005 0.001

x_α 2.072 2.706 3.841 5.024 6.635 7.879 10.828

组卷：21引用：3难度：0.5

解析

22．设函数
f
（
x
）
=
a
x
2
+
lnx
（
a
≠
0
）
，g（x）=x³-2x²+1．
（1）讨论函数f（x）的单调性；
（2）如果对于任意的x₁，
x
2
∈
[
1
2
，
2
]
，都有x₁f（x₁）≥g（x₂）成立，试求a的取值范围．
组卷：59引用：3难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

	属于“高分选手”	不属于“高分选手”	合计
男生
女生
合计

α	0.150	0.100	0.050	0.025	0.010	0.005	0.001
x_α	2.072	2.706	3.841	5.024	6.635	7.879	10.828

2022-2023学年河北省唐山市曹妃甸一中高二（下）期末数学试卷

一、单选题（本题共8小题，每小题5分，共40分）

1．（x2+3x）5的展开式中x4的系数是（ ）

2．已知函数f（x）的导函数为f′（x），且满足f（x）=2xf′（1）+lnx,则f′（2）=（ ）

3．某市一次高三模拟考试一共有3.2万名考生参加，他们的总分ξ服从正态分布N（480，σ2），若P（430≤ξ≤530）=0.78，则总分高于530分的考生人数为（ ）

4．5名学生参加数学建模活动，目前有3个不同的数学建模小组，每个小组至少分配1名学生，至多分配3名学生，则不同的分配方法种数为（ ）

5．（1+x）3+（1+x）4+⋯+（1+x）9的展开式中x3的系数是（ ）

6．已知C0n+2C1n+22C2n+23C3n+⋯+2nCnn=81，则C1n+C2n+C3n+⋯+Cnn等于（ ）

四、解答题（本题共6小题，17题10分，其余每题12分，共70分，解答应写出文字说明、证明过程或演算步骤）

22．设函数f（x）=ax2+lnx（a≠0），g（x）=x3-2x2+1．（1）讨论函数f（x）的单调性；（2）如果对于任意的x1，x2∈[12，2]，都有x1f（x1）≥g（x2）成立，试求a的取值范围．

1．（x²+
3
x
）⁵的展开式中x⁴的系数是（　　）

2．已知函数f（x）的导函数为f′（x），且满足f（x）=2xf′（1）+lnx,则f′（2）=（　　）

3．某市一次高三模拟考试一共有3.2万名考生参加，他们的总分ξ服从正态分布N（480，σ²），若P（430≤ξ≤530）=0.78，则总分高于530分的考生人数为（　　）

4．5名学生参加数学建模活动，目前有3个不同的数学建模小组，每个小组至少分配1名学生，至多分配3名学生，则不同的分配方法种数为（　　）

5．（1+x）³+（1+x）⁴+⋯+（1+x）⁹的展开式中x³的系数是（　　）

6．已知
C
0
n
+
2
C
1
n
+
2
2
C
2
n
+
2
3
C
3
n
+
⋯
+
2
n
C
n
n
=
81
，则
C
1
n
+
C
2
n
+
C
3
n
+
⋯
+
C
n
n
等于（　　）

22．设函数
f
（
x
）
=
a
x
2
+
lnx
（
a
≠
0
）
，g（x）=x³-2x²+1．
（1）讨论函数f（x）的单调性；
（2）如果对于任意的x₁，
x
2
∈
[
1
2
，
2
]
，都有x₁f（x₁）≥g（x₂）成立，试求a的取值范围．