2023-2024学年天津市武清区杨村一中高二（上）第一次月考数学试卷

一、选择题：本大题共9小题，每小题5分，共45分.

• 1．已知直线y=kx+3的倾斜角为60°，则实数k的值为（　　）

  A． - 3 2

  B． 3

  C． - 3 3

  D． - 3
  组卷：81引用：2难度：0.7

  解析

• 2．若向量

  a

  =（2，0，-1），向量

  b

  =（0，1，-2），则2

  a

  -

  b

  =（　　）

  A．（-4，1，-4）

  B．（-4，1，0）

  C．（4，-1，0）

  D．（4，-1，-4）
  组卷：1880引用：21难度：0.9

  解析

• 3．圆O₁：（x-1）²+y²=1与圆O₂：x²+（y+2）²=4的位置关系是（　　）

  A．外离

  B．外切

  C．相交

  D．内切
  组卷：131引用：3难度：0.6

  解析

• 4．若直线l₁：ax+（a+2）y+2=0与直线l₂：x+ay-2=0平行，则a=（　　）

  A．2

  B．-1

  C．2或-1

  D．-2或1
  组卷：310引用：6难度：0.8

  解析

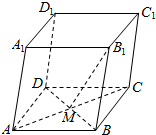• 5．如图，平行六面体ABCD-A₁B₁C₁D₁中，AC与BD交于点M，设

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则

  B

  1

  M

  =（　　）

  A． - 1 2 a - 1 2 b - c

  B． 1 2 a + 1 2 b - c

  C． 1 2 a - 1 2 b - c

  D． - 1 2 a + 1 2 b - c
  组卷：1173引用：18难度：0.7

  解析

• 6．已知点P（-1，1）在圆C：x²+y²+kx-2y+

  5

  4

  k=0外，则实数k的取值范围是（　　）

  A．k＞0

  B．k＜1或k＞4

  C．0＜k＜1或k＞4

  D．k＞4
  组卷：407引用：6难度：0.7

  解析

三、解答题：本大题共5个小题，共75分.

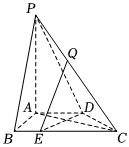• 19．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，其中AD∥BC，AB⊥AD，AB=AD=

  1

  2

  BC=2，PA=4，E为棱BC上的点，且BE=

  1

  4

  BC．
  （Ⅰ）求证：DE⊥平面PAC；
  （Ⅱ）求平面PAC与平面PCD所成角的余弦值；
  （Ⅲ）设Q为棱CP上的点（不与C、P重合），且直线QE与平面PAC所成角的正弦值为

  5

  5

  ，求

  CQ

  CP

  的值．
  组卷：251引用：5难度：0.5

  解析

• 20．已知圆O：x²+y²=1和点M（-1，-4）．
  （Ⅰ）过点M向圆O引切线，求切线的方程；
  （Ⅱ）求以点M为圆心，且被直线y=2x-12截得的弦长为8的圆M的方程；
  （Ⅲ）设P为（Ⅱ）中圆M上任意一点，过点P向圆O引切线，切点为Q，试探究：平面内是否存在一定点R，使得

  |

  PQ

  |

  |

  PR

  |

  为定值？若存在，请求出定点R的坐标，并指出相应的定值；若不存在，请说明理由．
  组卷：231引用：1难度：0.3

  解析