2022-2023学年四川省成都市树德中学光华校区高一(下)期末数学模拟试卷(3)
发布:2024/8/8 8:0:9
一、单选题(共40分)
-
1.已知复数z满足
,则z1+2i=2-i=( )z组卷:53引用:4难度:0.8 -
2.已知m,n是两条不同的直线,α,β是两个不同的平面,则( )
组卷:968引用:10难度:0.7 -
3.若向量
,a=(1,0),则向量b=(2,1)在向量a上的投影向量为( )b组卷:103引用:1难度:0.8 -
 4.已知一个直三棱柱的高为1,如图,其底面△ABC水平放置的直观图(斜二测画法)为△A′B′C′,其中O′A′=O′B′=O′C′=1,则该三棱柱的表面积为( )组卷:208引用:6难度:0.7
4.已知一个直三棱柱的高为1,如图,其底面△ABC水平放置的直观图(斜二测画法)为△A′B′C′,其中O′A′=O′B′=O′C′=1,则该三棱柱的表面积为( )组卷:208引用:6难度:0.7 -
5.在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.在鳖臑A-BCD中AB⊥平面BCD,BC⊥CD,且AB=BC=CD=2,则鳖臑A-BCD外接球的表面积为( )
组卷:335引用:4难度:0.6 -
6.已知
,若α∈(π,3π2),则tan2α的值是( )1+sin2α1+cos2α=92组卷:346引用:3难度:0.7 -
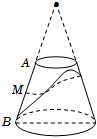 7.一圆台上底半径为5cm,下底半径为10cm,母线AB长为20cm,其中A在上底面上,B在下底面上,从AB中点M,拉一条绳子,绕圆台的侧面一周转到B点,则这条绳子最短长为( )组卷:295引用:5难度:0.7
7.一圆台上底半径为5cm,下底半径为10cm,母线AB长为20cm,其中A在上底面上,B在下底面上,从AB中点M,拉一条绳子,绕圆台的侧面一周转到B点,则这条绳子最短长为( )组卷:295引用:5难度:0.7
四、解答题(共70分)
-
21.在△ABC中,a,b,c分别为角A,B,C的对边,平面内点O满足(
+OA)•OB=(AB+OB)•OC=(BC+OC)•OA=0,且b2-2b+c2=0CA
(1)证明:点O为△ABC的外心;
(2)求的取值范围.BC•AO组卷:118引用:4难度:0.5 -
 22.如图,在四棱锥P-ABCD中,PB=PD,PA⊥PC,M,N分别为PA,BC的中点底面四边形ABCD是边长为2的菱形,且∠DAB=60°,AC交BD于点O.
22.如图,在四棱锥P-ABCD中,PB=PD,PA⊥PC,M,N分别为PA,BC的中点底面四边形ABCD是边长为2的菱形,且∠DAB=60°,AC交BD于点O.
(1)求证:MN∥平面PCD;
(2)二面角B-PC-D的平面角为θ,若.cosθ=-17
①求PA与底面ABCD所成角的大小;
②求点N到平面CDP的距离.组卷:274引用:3难度:0.6


