当前位置：试卷中心 > 试卷详情

2022-2023学年重庆实验外国语学校九年级（上）第二次月考数学试卷

发布：2024/9/7 3:0:8

一、选择题（本大题12个小题，每题4分，共48分）

1．下列4个图形中，既是中心对称图形又是轴对称的图形是（　　）
A． B． C． D．
组卷：115引用：7难度：0.8
解析
2．下列计算正确的是（　　）
A．a⁶÷a³+a²=2a² B．a²•a⁴=a⁸
C．2a+3b=5ab D．（-2a²b）3=-8a⁶b³
组卷：67引用：3难度：0.7
解析

3．下列调查中适合全面调查的是（　　）

A．调查球迷观看卡塔尔世界杯足球比赛的时间

B．调查某工厂生产的一批灯管的使用寿命

C．了解我校初三（1）班同学对电影《独行月球》的喜爱程度

D．了解重庆市初三学生名著阅读情况

组卷：152引用：3难度：0.8

解析

4．估计
3
21
×
1
3
的值应在（　　）
A．7和8之间 B．8和9之间 C．6和7之间 D．9和10之间
组卷：39引用：3难度：0.6
解析
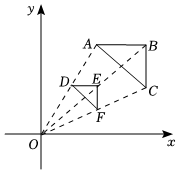5．如图，△ABC中，A（4，8），以原点为位似中心，将△ABC缩小后得到△DEF，若D（2，4），△DEF的面积为3，则△ABC的面积为（　　）
A．6 B．9 C．12 D．16
组卷：142引用：3难度：0.6
解析
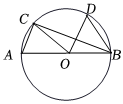6．已知AB为⊙O的直径，C为圆周上一点，AC∥DO，∠DBC=32°，则∠ABC的度数为
（　　）
A．22° B．24° C．26° D．28°
组卷：128引用：2难度：0.7
解析

7．下列四个命题中，是真命题的是（　　）

A．有理数与数轴上的点是一一对应的

B．三角形的一个外角大于任何一个内角

C．两条直线被第三条直线所截，同旁内角互补

D．平面内点A（-1，2）与点B（-1，-2）关于x轴对称

组卷：543引用：6难度：0.7

解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题6个小题，17题6分，18-22题每题10分，共56分）：解答时每小题都必须写出

21．四位数M各数位上的数字均不为零，把M的各个数位上的数字相加的和记为k,把M的千位数字与个位数字的乘积减去百位数字与十位数字的乘积所得的差记为n,若k恰好是|n|的整数倍，即p=k÷|n|，则称M是“k级积差数”，整数p为M的“积差商”．
例如：M=2143，∵k=2+1+4+3=10，n=2×3-1×4=2，p=10÷2=5；∴2143是“10级积差数”，“积差商p”为5．
又如：M=1738，∵k=1+7+3+8=19，n=1×8-7×3=-13，p=19÷|-13|不是整数；∴1738不是“k级积差数”．
（1）判断2358，9243是否为“k级积差数”，并说明理由；
（2）若M为“16级积差数”，M的“积差商p”也为16，M的千位与百位数字之和能被9整除，求所有满足条件的M．
组卷：72引用：1难度：0.7
解析
22．如图，在平面直角坐标系中，抛物线y=-
1
6
x²+bx+c与x轴交于A、B（4，0）两点，与y轴交于点C（0，4），连接AC．
（1）求该抛物线的解析式；
（2）如图1，点P为抛物线上第二象限内的一个动点，连接AP、OP，记AC和OP的交点为点D，过点O作AC的平行线交抛物线分别于点E、点F，点G为直线EF上的一个动点，连接GA、GD．当
S
△
APD
S
△
AGD
最大时，求
S
△
APD
S
△
AGD
的最大值和此时点P的坐标．
（3）如图2，将△AOC绕着点O顺时针旋转α（0°＜α＜90°）得到△A₁OC₁使得OC₁∥AC，点M是x轴上的一个动点，点N是平面内任意一点．是否存在这样的点M、N，使得以点A₁、C₁、M、N为顶点的四边形是以A₁M为一边的菱形．若存在，请直接写出点N的横坐标；若不存在，请说明理由．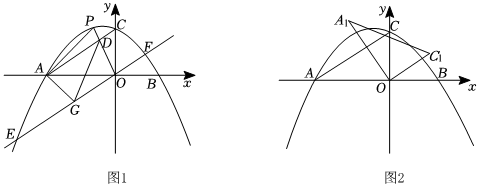
组卷：284引用：1难度：0.3
解析