当前位置：试卷中心 > 试卷详情

2021-2022学年四川省成都市新津实验高级中学高二（上）期中数学试卷

发布：2024/9/26 9:0:2

1．直线
3
x+y+2=0的倾斜角α是（　　）
A．
π
3
B．
π
6
C．
2
π
3
D．-
π
3
组卷：155引用：12难度：0.9
解析
2．直线ax+y+1=0与直线4x+ay-2=0平行，则a的值为（　　）
A．-2 B．2 C．±2 D．0
组卷：79引用：4难度：0.8
解析
3．到点
（
-
2
3
，
0
）
和
（
2
3
，
0
）
的距离之和为8的点的轨迹方程为（　　）
A．
x
2
16
+
y
2
4
=
1
B．
x
2
12
+
y
2
4
=
1
C．
x
2
16
+
y
2
12
=
1
D．
x
2
12
+
y
2
16
=
1
组卷：17引用：3难度：0.7
解析
4．已知点P（x₀，y₀）和点A（1，2）在直线l：3x+2y-8=0的异侧，则（　　）
A．3x₀+2y₀＞0 B．3x₀+2y₀＜0 C．3x₀+2y₀＜8 D．3x₀+2y₀＞8
组卷：68引用：11难度：0.9
解析
5．如果关于x的不等式x²＜ax+b的解集是{x|1＜x＜3}，那么b^a等于（　　）
A．-81 B．81 C．-64 D．64
组卷：1941引用：7难度：0.7
解析
6．若点（2，2）到直线x-y+a=0的距离是
2
2
，则实数a的值为（　　）
A．1 B．-1 C．0或-1 D．-1或1
组卷：990引用：3难度：0.9
解析
7．已知过点P（2，2）的直线与圆（x-1）²+y²=5相切，且与直线ax-y+1=0垂直，则a=（　　）
A．
-
1
2
B．1 C．2 D．
1
2
组卷：2562引用：89难度：0.7
解析

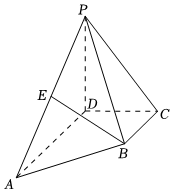21．如图，四棱锥P-ABCD满足∠ADC=∠BCD=90°，AD=2BC，PD⊥底面ABCD．
（1）设点E为PA的中点，证明：BE∥平面PDC；
（2）设平面PAD与平面PBC的交线为l,证明：平面PBC⊥平面PDC．
组卷：8引用：1难度：0.6
解析
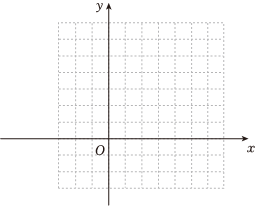22．若x,y满足约束条件
x
+
y
≥
1
-
x
+
y
≤
1
2
x
-
y
≤
2
，画出可行域，并回答：
（1）求目标函数
z
=
1
2
x
-
y
+
1
2
的最值；
（2）求目标函数z=x²+y²-10y+25的最小值；
（3）求目标函数
z
=
2
y
+
1
x
+
1
的范围．
组卷：6引用：1难度：0.5
解析

A． x 2 16 + y 2 4 = 1	B． x 2 12 + y 2 4 = 1
C． x 2 16 + y 2 12 = 1	D． x 2 12 + y 2 16 = 1

1．直线3x+y+2=0的倾斜角α是（ ）