2022-2023学年湖北省黄冈市浠水一中高一（下）期末数学试卷

一、单项选择题（本题共8小题，每小题5分，共40分.）

• 1．已知复数z=2+i+（1-i）x是纯虚数，则实数x=（　　）

  A．-2

  B．-1

  C．0

  D．1
  组卷：75引用：4难度：0.8

  解析

• 2．树人中学高一年级8名学生某次考试的数学成绩（满分150分）分别为85，90，93，99，101，103，116，130，则这8名学生数学成绩的第75百分位数为（　　）

  A．102

  B．103

  C．109.5

  D．116
  组卷：75引用：2难度：0.8

  解析

• 3．在△ABC中，角A，B，C的对边分别为a,b,c,acosC+ccosA=c,则△ABC的形状为（　　）

  A．直角三角形	B．等边三角形
  C．等腰三角形	D．等腰直角三角形
  组卷：153引用：5难度：0.7

  解析

• 4．设α，β为两个不同的平面，m,n为两条不同的直线，下列命题正确的是（　　）

  A．若m∥α，n⊂α，则m∥n

  B．若α∥β，m∥α，n∥β，则m∥n

  C．若m⊥β，n∥β，则m⊥n

  D．若α⊥β，α∩β=m,n⊥m,则n⊥α
  组卷：46引用：2难度：0.6

  解析

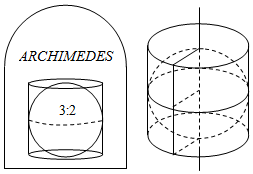• 5．阿基米德（Archimedes,公元前287年一公元前212年）是古希腊伟大的数学家、物理学家和天文学家．他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二，并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现，后人按照他生前的要求，在他的墓碑上刻着一个圆柱容器里放了一个球，如图，该球顶天立地，四周碰边，圆柱的底面直径与高都等于球的直径，若球的体积为36π，则圆柱的表面积为（　　）

  A．36π

  B．45π

  C．54π

  D．63π
  组卷：275引用：9难度：0.8

  解析

• 6．在△ABC中，角A，B，C所对应的边分别是a,b,c,若

  C

  =

  π

  6

  ，b=2c=2，则△ABC的面积为（　　）

  A． 3 2

  B．1

  C． 3

  D．2
  组卷：67引用：2难度：0.7

  解析

• 7．已知A，B，C，P为球O的球面上的四个点，△ABC为边长为

  4

  3

  的等边三角形，以A，B，C，P为顶点的三棱锥的体积的最大值为

  32

  3

  ，则球O的表面积为（　　）

  A．100π

  B．72π

  C．64π

  D．48π
  组卷：222引用：3难度：0.5

  解析

四、解答题（本题共6小题，共70分.）

• 21．已知△ABC的内角A，B，C的对边分别是a,b,c,△ABC的面积为S，且满足（2b-c）cosA=acosC，bcosC+ccosB=1．
  （1）求A和a的大小；
  （2）若△ABC为锐角三角形，求△ABC的面积S的取值范围．
  组卷：151引用：2难度：0.5

  解析

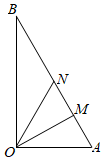• 22．如图所示，某镇有一块空地△OAB，其中OA=3km,OB=3

  3

  km,∠AOB=90°．当地镇政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖△OMN，其中M，N都在边A，B上，且∠MON=30°，挖出的泥土堆放在△OAM地带上形成假山，剩下的△OBN地带开设儿童游乐场．为安全起见，需在△OAN的一周安装防护网．
  （1）当AM=

  3

  2

  km时，求防护网的总长度；
  （2）若要求挖人工湖用地△OMN的面积是堆假山用地△OAM的面积的

  3

  倍，试确定∠AOM的大小；
  （3）为节省投入资金，人工湖△OMN的面积要尽可能小，问如何设计施工方案，可使△OMN的面积最小？最小面积是多少？
  组卷：978引用：13难度：0.3

  解析