2022-2023学年浙江省宁波市慈溪市高一（下）期末数学试卷
发布：2024/6/28 8:0:9
一、选择题：本题共8小题，每小题5分，共40分。
-
1．已知复数z满足z•i=2+i,则z=（ ）
组卷：135引用：2难度：0.9 -
2．已知向量
，AB=（1，3），点A（-1，2），则点C的坐标为（ ）BC=（2，1）组卷：115引用：2难度：0.7 -
3．据慈溪市气象局统计，2022年我市每月平均最高气温（单位：摄氏度）分别为12，11，10，20，23，28，36，36，31，24，23，19，这组数据的第60百分位数是（ ）
组卷：91引用：2难度：0.7 -
4．据长期观察，某学校周边早上6时到晚上18时之间的车流量y（单位：辆）与时间t（单位：h）满足如下函数关系式：
（A为常数，6≤t≤18）．已知早上8：30（即t=8.5h）时的车流量为500辆，则下午15：30（即t=15.5h）时的车流量约为（参考数据：y=Asin（π4t-138π）+300，2≈1.41）（ ）3≈1.73组卷：74引用：3难度：0.7 -
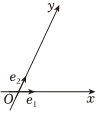5．如图，设Ox,Oy是平面内相交成θ角（0＜θ＜π）的两条数轴，，e1分别是与x轴、y轴正方向同向的单位向量．若向量e2，则称有序实数对（x,y）为向量OQ=xe1+ye2在坐标系Oxy中的坐标，已知在该坐标系下，向量OQ，OM=（1，2），若ON=（2，1），则cosθ=（ ）OM⊥ON组卷：78引用：1难度：0.7 -
6．已知某圆锥的底面积为16π，且它的外接球的体积为
，则该圆锥的侧面积为（ ）5003π组卷：159引用：2难度：0.5 -
7．从2023年6月开始，浙江省高考数学使用新高考全国数学I卷，与之前浙江高考数学卷相比最大的变化是出现了多选题．多选题规定：在每题给出的四个选项中，有多项符合题目要求，全部选对得5分，有选错的得0分，部分选对且没有选错的得2分．若某题多选题正确答案是BCD，某同学不会做该题的情况下打算随机选1个到3个选项作为答案，每种答案都等可能（例如，选A，AB，ABC是等可能的），则该题得2分的概率是（ ）
组卷：135引用：4难度：0.7
四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或验算步骤.
-
21．在①2a-b=2ccosB，②
这两个条件中任选一个，补充在下面问题中，并求解（1）、（2）的答案．3c•cosA+asinC=3b
问题：在△ABC中，三个内角A，B，C所对的边分别是a,b,c,已知______
（1）求角C；
（2）若点D是满足2AD=DB，且CD=1，求△ABC的面积的最大值．
（注：如果选择两个条件分别解答，则按第一个解答计分．）组卷：155引用：3难度：0.6 -
22．如图，在矩形ABCD中，AB=1，
，M是线段AD上的一动点，将△ABM沿着BM折起，使点A到达点A′的位置，满足点A′∉平面BCDM且点A′在平面BCDM内的射影E落在线段BC上．BC=3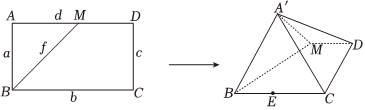
（1）当点M与端点D重合时，证明：A′B⊥平面A′CD；
（2）求三棱锥E-A′BM的体积的最大值；
（3）设直线CD与平面A′BM所成的角为α，二面角A′-BM-C的平面角为β、求sin2α•cosβ的最大值．组卷：243引用：4难度：0.5
