2022-2023学年广东省江门市台山市碧桂园学校高二(上)期中数学试卷
发布:2024/9/25 12:0:1
一、单项选择题(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项符合题目要求)
-
1.已知两个向量
,且a=(2,-1,3),b=(4,m,n),则m+n的值为( )a∥b组卷:488引用:29难度:0.9 -
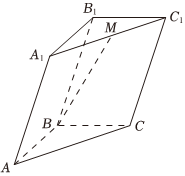 2.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若=AB,a=BC,b=AA1,则c可表示为( )BM组卷:360引用:8难度:0.7
2.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若=AB,a=BC,b=AA1,则c可表示为( )BM组卷:360引用:8难度:0.7 -
3.过点A(-
,3)与点B(-2,2)的直线的倾斜角为( )3组卷:254引用:11难度:0.8 -
4.“m=-1”是“直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直”的( )
组卷:77引用:11难度:0.9 -
5.直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是( )
组卷:11395引用:92难度:0.5 -
6.方程
+(x-2)2+y2=10,化简的结果是( )(x+2)2+y2组卷:585引用:9难度:0.7 -
7.过点(1,0)且倾斜角为30°的直线被圆(x-2)2+y2=1所截得的弦长为( )
组卷:6引用:1难度:0.7
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
21.已知椭圆
焦点为F1(-2,0),F2(2,0)且过点(-2,3),椭圆上一点P到两焦点F1,F2的距离之差为2.x2a2+y2b2=1(a>b>0)
(1)求椭圆的标准方程;
(2)求△PF1F2的面积.组卷:1675引用:8难度:0.8 -
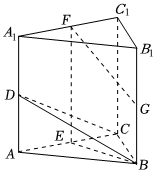 22.如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC==2.5,AC=AA1
22.如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC==2.5,AC=AA1
(1)求证:AC⊥平面BEF;
(2)求二面角B-CD-C1的余弦值.组卷:142引用:4难度:0.6


