2022-2023学年河南省南阳市宛城区八年级(下)期末数学试卷
发布:2024/6/30 8:0:9
一、选择题(每小题3分,共30分.)(下列各小题只有一个答案是正确的.)
-
1.分式
有意义的条件是( )x+2x-1组卷:112引用:3难度:0.8 -
2.若双曲线
经过点A(2,y1),B(5,y2),则y1与y2的大小关系为( )y=10x组卷:35引用:1难度:0.5 -
3.调查某少年足球队全体队员的年龄,得到数据结果如下表:
则该足球队队员年龄的众数是( )年龄/岁 11 12 13 14 15 人数 3 4 7 2 2 组卷:580引用:6难度:0.8 -
4.在▱ABCD中,在∠A+∠B+∠C=220°,则∠B的度数是( )
组卷:260引用:5难度:0.5 -
5.“无风才到地,有风还满空.缘渠偏似雪,莫近鬓毛生”是唐朝诗人雍裕之描写每年四月许多地方杨絮、柳絮如雪花般漫天飞舞的诗句,柳絮带给人们春天的讯息外也让人们不堪其扰,据测定,杨絮纤维的直径约为0.00000105m,该数值用科学记数法表示为( )
组卷:158引用:7难度:0.7 -
6.依据所标数据,下列一定为平行四边形的是( )
组卷:3039引用:45难度:0.5 -
7.将直线y=5x向下平移2个单位长度,所得直线的表达式为( )
组卷:1679引用:12难度:0.6
三、解答题(共75分)
-
22.综合与实践
综合实践课上,老师让同学们以“三角形纸片的折叠”为主题开展数学活动,类比探究一种特殊四边形的定义、性质、判定和应用.
【操作发现】
对折△ABC(AB>AC),使点C落在边AB上的点E处,得到折痕AD,把纸片展平,如图1.小明发现四边形AEDC满足:AE=AC,DE=DC.查阅相关资料得知,像这样的有两组邻边分别相等的四边形叫作“筝形”.
【类比探究】
借助学习几何图形的经验,通过观察、实验、归纳、类比、猜想、证明等方法,小宛同学对“筝形”的性质和判定方法进行了探究.
请根据示例图形,对比表格内容完成相关问题.
(1)表格中①、②处应分别填写的内容是:四边形 示例图形 对称性 边 角 对角线 平行
四边形
是中心对称图形 两组对边分别平行,两组对边分别相等. 两组对角分别相等 对角线互相平分. 菱形 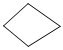
① 两组邻边分别相等 有一组对角相等 ②
①;②;
(2)证明筝形有关对角线的性质.
已知:如图2,在筝形AEDC中,AE=AC,DE=DC,对角线AD、EC交于点O.
求证:;
证明:
(3)写出这类“筝形”的一条判定方法(除“筝形”的定义外):.
【迁移应用】
(4)如图3,在Rt△ABC中,∠A=90°,∠B=30°,点D、E分别是边BC、AB上的动点,当四边形AEDC为筝形时,直接写出∠BDE的度数.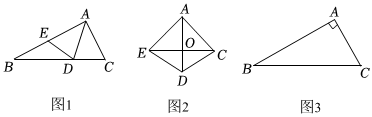 组卷:188引用:3难度:0.3
组卷:188引用:3难度:0.3 -
23.端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A粽子能够畅销.根据预测,A粽子的进价节前是节后的1.2倍,节前用150元购进A粽子的数量比节后用相同金额购进的数量少10个,根据以上信息,解答下列问题:
(1)该商场节后每个A粽子的进价是多少元?
(2)如果该商场在节前和节后共购进A粽子500个,且总费用不超过1400元,并按照节前每个8元,节后每个5元全部售出,那么该商场节前购进多少个A粽子获得利润最大?最大利润是多少?组卷:157引用:3难度:0.6


