2022-2023学年吉林省“BEST合作体”高一（下）期末数学试卷

一、选择题：共60分

• 1．若复数z满足

  z

  -

  1

  z

  +

  1

  =

  i

  2023

  ，则

  |

  z

  |

  =（　　）

  A．2

  B．2023

  C． 2023

  D．1
  组卷：113引用：6难度：0.8

  解析

• 2．已知直线l的方向向量

  a

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，平面α的一个法向量为

  n

  =

  （

  1

  ，

  1

  ，-

  6

  ）

  ，则直线l与平面α所成的角为（　　）

  A．120°

  B．60°

  C．30°

  D．150°
  组卷：416引用：7难度：0.9

  解析

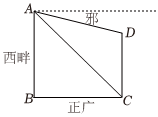• 3．《九章算术》是中国古代一部数学专著，其中的“邪田”为直角梯形，上、下底称为“畔”，高称为“正广”，非高腰边称为“邪”．如图所示，邪长为

  4

  3

  ，东畔长为

  2

  7

  ，在A处测得C，D两点处的俯角分别为49°和19°，则正广长约为（注：sin41°≈0.66）（　　）

  A．6.6

  B．3.3

  C．4

  D．7
  组卷：110引用：5难度：0.8

  解析

• 4．如图所示，M是四面体OABC的棱BC的中点，点N在线段OM上，点P在线段AN上，且AP=3PN，

  ON

  =

  2

  3

  OM

  ，设

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，则下列等式成立的是（　　）

  A． OP = 1 4 a + 1 4 b + 1 4 c	B． AN = a + 1 3 b + 1 3 c
  C． AP = - 3 4 a + 1 4 b - 1 4 c	D． OM = 1 2 b - 1 2 c
  组卷：277引用：3难度：0.8

  解析

• 5．在△ABC中，角A，B，C所对的边分别为a,b,c,且

  c

  =

  8

  ，

  B

  =

  π

  6

  ．若△ABC有两解，则b的值可以是（　　）

  A．4

  B．6

  C．8

  D．10
  组卷：376引用：9难度：0.7

  解析

• 6．关于用统计方法获取、分析数据，下列结论错误的是（　　）

  A．质检机构为检测一大型超市某商品的质量情况，合理的调查方式为抽样调查

  B．若甲、乙两组数据的标准差满足S甲＜S乙，则可以估计甲比乙更稳定

  C．若数据x1，x2，x3，⋯，xn的平均数为 x ，则数据yi=axi-b（i=1，2，3，⋯，n）的平均数为 a x - b

  D．为了解高一学生的视力情况，现有高一男生200人，女生400人，按性别进行分层抽样，样本量按比例分配，若从女生中抽取的样本量为80，则男生样本容量为60
  组卷：111引用：7难度：0.8

  解析

• 7．某中学举行疾病防控知识竞赛，其中某道题甲队答对该题的概率为

  3

  4

  ，乙队和丙队答对该题的概率都是

  2

  3

  ．若各队答题的结果相互独立且都进行了答题．则甲、乙、丙三支竞赛队伍中恰有一支队伍答对该题的概率为（　　）

  A． 1 2

  B． 1 3

  C． 7 36

  D． 1 6
  组卷：306引用：7难度：0.8

  解析

三、解答题：本题共6小题，共70分。解答题应写出文字说明、证明过程或演算步骤。

• 21．一个口袋内装有形状，大小相同，编号为1，2，3的3个白球和编号为a的1个黑球．
  （1）从中一次性摸出2个球，求摸出的2个球都是白球的概率；
  （2）从中连续取两次，每次取一球后放回，甲、乙约定：若取出的两个球中至少有1个黑球，则甲胜，反之，则乙胜．你认为此游戏是否公平？说明你的理由．
  组卷：43引用：2难度：0.7

  解析

• 22．已知在△ABC中，角A，B，C的对边分别为a,b,c,∠A=150°，点D满足

  CD

  =

  2

  DB

  ，且

  sin

  ∠

  BAD

  b

  +

  sin

  ∠

  CAD

  c

  =

  3

  2

  a

  ．
  （1）求证：

  AD

  =

  1

  3

  a

  ；
  （2）求

  si

  n

  2

  A

  sin

  B

  sin

  C

  的值．
  组卷：58引用：3难度：0.5

  解析