2022-2023学年四川省巴中市通江中学高二（上）期中数学试卷（文科）

一.选择题（共12小题，每题5分，共60分）

• 1．命题“∀x∈R，

  （

  1

  3

  ）

  x

  ＞0”的否定是（　　）

  A．∃x∈R， （ 1 3 ） x ＜ 0	B．∀x∈R， （ 1 3 ） x ≤ 0
  C．∀x∈R， （ 1 3 ） x ＞ 0	D．∃x∈R， （ 1 3 ） x ≤ 0
  组卷：58引用：13难度：0.9

  解析

• 2．设直线l：x-

  3

  y+b=0的倾斜角为α，则α=（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  组卷：100引用：4难度：0.8

  解析

• 3．若直线l：ax-by+1=0平分圆C：x²+y²+2x-4y+1=0的周长，则a+2b的值为（　　）

  A．1

  B．-1

  C．4

  D．-4
  组卷：101引用：2难度：0.7

  解析

• 4．已知直线l、m、n与平面α、β，下列命题正确的是（　　）

  A．若α∥β，l⊂α，n⊂β，则l∥n	B．若α⊥β，l⊂α，则l⊥β
  C．若l⊥n,m⊥n则l∥m	D．若l⊥α，l∥β，则α⊥β
  组卷：660引用：17难度：0.8

  解析

• 5．已知点A（2，-3），B（-3，-2）．若直线l：mx+y-m-1=0与线段AB相交，则实数m的取值范围是（　　）

  A．（-∞，- 3 4 ]∪[4，+∞）	B．（-∞，-4]∪[ 3 4 ，+∞）
  C．[- 3 4 ，4]	D．[-4， 3 4 ]
  组卷：752引用：9难度：0.8

  解析

• 6．在正方体ABCD-A₁B₁C₁D₁中，E，F分别为AB，BC的中点，则（　　）

  A．平面B1EF⊥平面BDD1	B．平面B1EF⊥平面A1BD
  C．平面B1EF∥平面A1AC	D．平面B1EF∥平面A1C1D
  组卷：3780引用：11难度：0.6

  解析

• 7．在正方体ABCD-A₁B₁C₁D₁中，P为B₁D₁的中点，则直线PB与AD₁所成的角为（　　）

  A． π 2

  B． π 3

  C． π 4

  D． π 6
  组卷：5078引用：39难度：0.7

  解析

三.解答题（共6小题，第17题10分，其余每题12分，共70分，解答题应写出文字说明，证明过程或演算步骤）

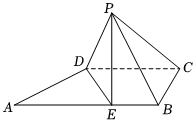• 21．如图，直角梯形ABCD中，AB∥CD，AB⊥BC，E为AB上的点，且AD=AE=DC=2，BE=1，将△ADE沿DE折叠到P点，使PC=PB．
  （1）求证：平面PDE⊥平面ABCD；
  （2）求四棱锥P-EBCD的体积．
  组卷：64引用：3难度：0.4

  解析

• 22．已知圆C过点A（1，2），B（2，1），且圆心C在直线y=-x上．P是圆C外的点，过点P的直线l交圆C于M，N两点．
  （1）求圆C的方程；
  （2）若点P的坐标为（0，-3），求证：无论l的位置如何变化|PM|•|PN|恒为定值；（几何法不给分）
  （3）对于（2）中的定值，使|PM|•|PN|恒为该定值的点P是否唯一？若唯一，请给予证明；若不唯一，写出满足条件的点P的集合．（几何法不给分）
  组卷：86引用：6难度：0.4

  解析