2022-2023学年广东省广州市华南师大附中高一（下）期末数学试卷

一、单选题：本大题共8小题，每小题3分，满分24分，在每小题给出的四个选项中，只有一项符合题目要求．

• 1．已知单位向量

  a

  ，

  b

  满足

  a

  ⊥

  b

  ，则

  a

  •（

  a

  -

  b

  ）=（　　）

  A．0

  B． 1 2

  C．1

  D．2
  组卷：349引用：6难度：0.8

  解析

• 2．已知复数z满足

  z

  =

  2

  1

  -

  i

  +

  i

  ，则|z|=（　　）

  A．1

  B． 2

  C． 3

  D． 5
  组卷：307引用：13难度：0.8

  解析

• 3．已知正四棱锥的底面边长是6，高为

  7

  ，则该正四棱锥的体积为（　　）

  A． 6 7

  B． 12 7

  C． 24 7

  D． 36 7
  组卷：309引用：3难度：0.7

  解析

• 4．某校高一、高二、高三的住校生人数分别为120，180，150，为了解他们对学校宿舍的满意程度，按人数比例用分层抽样的方法抽取90人进行问卷调查，则高一、高二、高三被抽到的住校生人数分别为（　　）

  A．12，18，15

  B．20，40，30

  C．25，35，30

  D．24，36，30
  组卷：302引用：5难度：0.8

  解析

• 5．在一次抛硬币的试验中，某同学用一枚质地均匀的硬币做了800次试验，发现正面朝上出现了440次，那么出现正面朝上的频率和概率分别为（　　）

  A．0.55，0.55

  B．0.55，0.5

  C．0.5，0.5

  D．0.5，0.55
  组卷：293引用：6难度：0.7

  解析

• 6．如图甲，在梯形ABCD中，AB∥CD，CD=2AB，E、F分别为AD、CD的中点，以AF为折痕把△ADF折起，使点D不落在平面ABCF内（如图乙），那么在以下3个结论中，正确结论的个数是（　　）
  ①AF∥平面BCD；②BE∥平面CDF；③CD∥平面BEF．

  A．0

  B．1

  C．2

  D．3
  组卷：778引用：3难度：0.5

  解析

• 7．如图，在太极图中，A，B分别为太极图中的最低点和最高点，AB经过大圆和小圆的圆心，且两个小圆的圆心是线段AB的两个四等分点（异于AB中点），过A作黑色小圆的切线，切点为C，则向量

  AB

  在向量

  AC

  上的投影向量为（　　）

  A． 6 AC

  B． 4 AC

  C． 4 2 AC

  D． 3 2 AC
  组卷：137引用：3难度：0.7

  解析

四、解答题：本大题共6小题，满分52分．解答应写出文字说明、证明过程或演算过程．

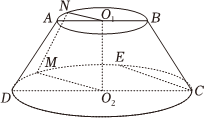• 21．已知圆台O₁O₂轴截面ABCD，圆台的上底面圆半径与高都等于1，下底面圆半径等于2，点E为下底圆弧

  ˆ

  CD

  的中点，点N为上底圆周上靠近点A的弧

  ˆ

  AB

  的四等分点，经过O₁、O₂，N三点的平面与弧

  ˆ

  CD

  交于点M，且E，M，N三点在平面ABCD的同侧．
  （1）判断平面O₁O₂MN与直线CE的位置关系，并证明你的结论；
  （2）P为下底圆周上左半部分（靠近D点）的一个动点，且与M点在CD的不同侧，当四棱锥P-ABCD的体积等于

  2

  时，求二面角N-PM-D的余弦值．
  组卷：217引用：1难度：0.4

  解析

• 22．已知向量

  a

  =

  （

  cos

  5

  x

  ,

  sin

  5

  x

  ）

  ，

  b

  =

  （

  2

  cos

  （

  x

  -

  π

  3

  ）

  ，

  2

  sin

  （

  x

  -

  π

  3

  ）

  ）

  ，令u（x）=

  a

  •

  b

  ．
  （1）求函数u（x）的对称轴方程；
  （2）设

  v

  （

  x

  ）

  =

  4

  cos

  （

  2

  x

  +

  π

  6

  ）

  ，当

  x

  ∈

  [

  -

  π

  6

  ，

  π

  12

  ]

  时，求函数f（x）=4u（x）-2λv（x）+6λ+5（λ∈R）的最小值g（λ）；
  （3）在（2）的条件下，若对任意的实数a,b且a＞b＞0，不等式

  t

  -

  （

  1

  a

  +

  1

  2

  b

  ）

  （

  a

  +

  2

  b

  ）

  ≤

  g

  （

  λ

  ）

  ≤

  2

  t

  +

  a

  2

  +

  1

  ab

  +

  1

  a

  （

  a

  -

  b

  ）

  对任意的λ∈[0，5]恒成立，求实数t的取值范围．
  组卷：922引用：5难度：0.1

  解析