2022-2023学年贵州省遵义市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每个小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知角α终边经过点P（-3，4），则cosα的值为（　　）

  A． - 4 5

  B． - 3 5

  C． 3 5

  D． 4 5
  组卷：635引用：10难度：0.9

  解析

• 2．已知i为虚数单位，则复数

  5

  i

  3

  +

  4

  i

  的虚部为（　　）

  A． 3 5

  B． - 3 5

  C． 3 5 i

  D． - 3 5 i
  组卷：42引用：3难度：0.8

  解析

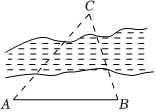• 3．如图所示，为测量河对岸一点C与岸边一点A之间的距离，已经测得岸边的A，B两点间的距离为m,∠CAB=α，∠CBA=β，则C，A间的距离为（　　）

  A． msinβ sinα	B． msinα sinβ
  C． msinβ sin （ α + β ）	D． msin （ α + β ） sinβ
  组卷：26引用：3难度：0.7

  解析

• 4．已知一个圆锥的底面半径为1，体积是

  3

  π

  3

  ，则其侧面展开图的圆心角为（　　）

  A． π 4

  B． π 3

  C． π 2

  D．π
  组卷：27引用：2难度：0.7

  解析

• 5．已知长方体ABCD-A₁B₁C₁D₁中，A₁B=2，AC=3，AA₁=

  3

  ，则直线A₁B与直线AC所成角的余弦值为（　　）

  A．- 3 6

  B．- 1 6

  C． 1 6

  D． 3 6
  组卷：44引用：2难度：0.6

  解析

• 6．已知

  sin

  （

  α

  +

  π

  6

  ）

  =

  1

  3

  ，则

  cos

  （

  2

  π

  3

  -

  2

  α

  ）

  =（　　）

  A． - 7 9

  B． 7 9

  C． - 4 2 9

  D． 4 2 9
  组卷：601引用：7难度：0.7

  解析

• 7．已知△ABC中，3AB=2AC，D为边BC上一点，满足sin∠CAD=2sin∠BAD，则

  BD

  DC

  =（　　）

  A． 1 3

  B． 1 2

  C． 3 2

  D．3
  组卷：66引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

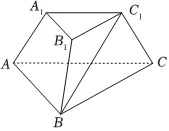• 21．如图，棱台ABC-A₁B₁C₁的底面ABC是正三角形，侧面ACC₁A₁⊥底面ABC，AA₁=A₁C₁=CC₁=1，AB=2．
  （1）求BC₁的长；
  （2）求直线AC与平面BCC₁B₁所成角的正弦值．
  组卷：44引用：2难度：0.6

  解析

• 22．已知向量

  u

  =

  （

  a

  ,

  b

  ）

  ，

  v

  =

  （

  c

  ,

  d

  ）

  ，其中a,b,c,d∈（0，+∞）．
  （1）若

  |

  u

  •

  v

  |

  =

  |

  u

  |

  |

  v

  |

  ，写出a,b,c,d之间应满足的关系式
  （2）求证：（a²+b²）（c²+d²）≥（ac+bd）²；
  （3）求代数式

  4

  x

  +

  13

  +

  2

  3

  -

  x

  的最大值，并求其取得最大值时x的值．
  组卷：9引用：2难度：0.5

  解析