2022-2023学年山东省青岛大学附中九年级（上）期中数学试卷

一、选择题（本题共8小题，每小题3分，共24分，在每小题的四个选项中，只有一项符合要求）

• 1．已知方程x²+mx+3=0的一个根是1，则m的值为（　　）

  A．4

  B．-4

  C．3

  D．-3
  组卷：810引用：14难度：0.9

  解析

• 2．下列各组的四条线段a,b,c,d是成比例线段的是（　　）

  A．a=4，b=6，c=5，d=10	B．a=1，b=2，c=3，d=4
  C． a = 2 ，b=3，c=2， d = 3	D．a=2， b = 5 ， c = 2 3 ， d = 15
  组卷：3972引用：30难度：0.9

  解析

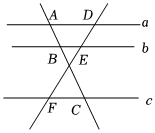• 3．如图，已知直线a∥b∥c,若AB=2，BC=3，EF=2.5，则DE=（　　）

  A． 3 5

  B． 5 3

  C． 4 15

  D． 15 4
  组卷：1614引用：10难度：0.8

  解析

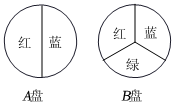• 4．用如图所示的A、B两个转盘进行“配紫色”游戏（红色和蓝色在一起配成紫色），A转盘是二等分，B转盘是三等分，分别转动两个转盘各一次（指针指向分界线则重新转动转盘），则配成紫色的概率为（　　）

  A． 1 6

  B． 1 4

  C． 1 3

  D． 1 2
  组卷：374引用：9难度：0.6

  解析

• 5．如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（　　）

  A．∠ABP=∠C

  B．∠APB=∠ABC

  C． AP AB = AB AC

  D． AB BP = AC CB
  组卷：16126引用：185难度：0.9

  解析

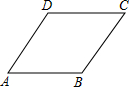• 6．如图，菱形ABCD的周长为16，∠A：∠B=1：2，则菱形的面积为（　　）

  A．2 3

  B．3 3

  C．4 3

  D．8 3
  组卷：280引用：7难度：0.7

  解析

• 7．如图，校园里一片小小的树叶，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm,那么BP的长度为（　　）cm.

  A． 5 5 - 5

  B． 5 + 5 5

  C． 15 - 5 5

  D． 15 + 5 5
  组卷：237引用：4难度：0.6

  解析

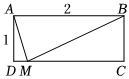• 8．如图，矩形ABCD中，AB=2，AD=1，点M在边CD上，若AM平分∠DMB，则DM的长是（　　）

  A．2- 3

  B． 3

  C．4 3

  D． 3 -1
  组卷：490引用：2难度：0.6

  解析

四、解答题：（本题共9道小题，满分74分）

• 23．【模型呈现：材料阅读】
  如图1，点B，C，E在同一直线上，点A，D在直线CE的同侧，△ABC和△CDE均为等边三角形，AE，BD交于点F．对于上述问题，存在结论（不用证明）：
  （1）△BCD≌△ACE；
  （2）△ACE可以看作是由△BCD绕点C旋转而成；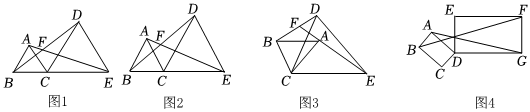
  
  【模型改编：问题解决】
  如图2，点A，D在直线CE的同侧，AB=AC，ED=EC，∠BAC=∠DEC=48°，直线AE，BD交于F．
  ①求证：△BCD∽△ACE；
  ②则∠AFB的度数．
  如图3：将△ABC绕点C顺时针旋转一定角度，
  ③则∠AFB的度数为

  ．
  ④若将“∠BAC=∠DEC=48°”改为“∠BAC=∠DEC=m°”，则∠AFB的度数为

  .（直接写结论）
  【模型拓广：问题延伸】
  如图4：在矩形ABCD和矩形DEFG中，AB=1，AD=ED=

  3

  ，DG=3，连接AG，BF，⑤则

  BF

  AG

  的值为

  ．
  组卷：364引用：4难度：0.2

  解析

• 24．如图，在矩形ABCD中，BD是对角线，AB=6cm,BC=8cm,点E从点D出发，沿DA方向匀速运动，速度是2cm/s；点F从点B出发，沿BD方向匀速运动，速度是1cm/s.两点同时出发，设运动时间为t（s）（0＜t＜4），请回答下列问题
  
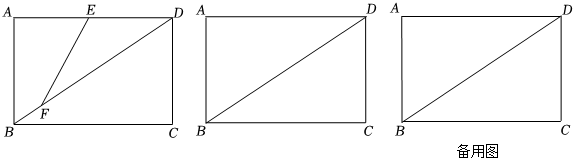
  （1）当t为何值时，EF∥AB？
  （2）设四边形ABFE的面积为S（cm²），求S与t之间的函数关系式；
  （3）当t为何值时，四边形ABFE的面积S等于矩形ABCD面积的

  3

  8

  ？
  （4）当t为

  时，△EFD是等腰三角形．
  组卷：371引用：3难度：0.4

  解析