【模型呈现：材料阅读】
如图1，点B，C，E在同一直线上，点A，D在直线CE的同侧，△ABC和△CDE均为等边三角形，AE，BD交于点F．对于上述问题，存在结论（不用证明）：
（1）△BCD≌△ACE；
（2）△ACE可以看作是由△BCD绕点C旋转而成；
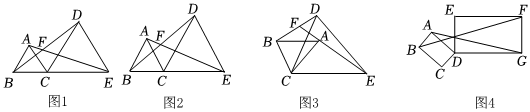
【模型改编：问题解决】
如图2，点A，D在直线CE的同侧，AB=AC，ED=EC，∠BAC=∠DEC=48°，直线AE，BD交于F．
①求证：△BCD∽△ACE；
②则∠AFB的度数．
如图3：将△ABC绕点C顺时针旋转一定角度，
③则∠AFB的度数为 114°114°．
④若将“∠BAC=∠DEC=48°”改为“∠BAC=∠DEC=m°”，则∠AFB的度数为 90°+m°290°+m°2.（直接写结论）
【模型拓广：问题延伸】
如图4：在矩形ABCD和矩形DEFG中，AB=1，AD=ED=3，DG=3，连接AG，BF，⑤则BFAG的值为 233233．
m
°
2
m
°
2
3
BF
AG
2
3
3
2
3
3
【考点】相似形综合题．
【答案】114°；90°+；
m
°
2
2
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/19 8:0:9组卷：364引用：4难度：0.2
相似题
-
1．（1）已知，直线AC与BD交于点O．
①如图1，若∠A=∠D，求证：AO•CO=BO•DO；
②如图2，若∠A+∠D=180°，求证：；ABCD=BOCO
（2）如图3，在△ABC中，∠A=60°，E为BD中点，且∠BEC=120°，DE：CD=1：n.则AB：CE=．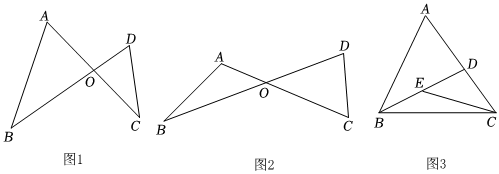
发布：2025/5/22 19:30:1组卷：288引用：1难度：0.1 -
2．如图，矩形ABCD中，AB=5，BC=4．点P在AD上运动（点P不与点A、D重合）将△ABP沿直线翻折，使得点A落在矩形内的点M处（包括矩形边界）．
（1）求AP的取值范围；
（2）连接DM并延长交矩形ABCD的AB边于点G，当∠ABM=2∠ADG时，求AP的长．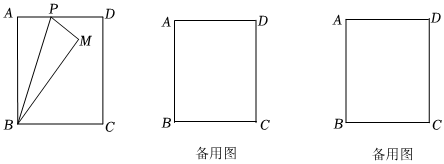
发布：2025/5/22 21:30:2组卷：1261引用：4难度：0.2 -
3．如图1，在Rt△ABC中，∠A=90°，AB=6，sinB=
．点D为AB的中点，过点D作射线DE∥BC交AC于点E，点M为射线DE上一动点，过点M作MN⊥BC于点N，点P为边AC上一点，连结NP，且满足45，设BN=x,NP=y.APBN=45
（1）求线段MN的长；
（2）求y关于x的函数表达式；
（3）如图2，连结MP．
①当△MNP为等腰三角形时，求x的值．
②以点M为旋转中心，将线段MP按顺时针方向旋转90°得线段MP′，当点P′落在BC边上时，求的值．NPAB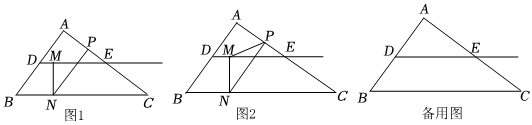
发布：2025/5/22 21:30:2组卷：571引用：6难度：0.1
