如图，在矩形ABCD中，BD是对角线，AB=6cm,BC=8cm,点E从点D出发，沿DA方向匀速运动，速度是2cm/s；点F从点B出发，沿BD方向匀速运动，速度是1cm/s.两点同时出发，设运动时间为t（s）（0＜t＜4），请回答下列问题
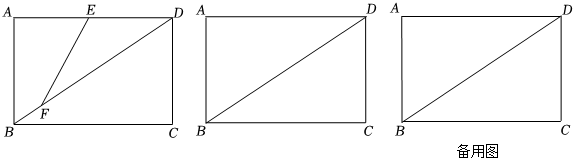
（1）当t为何值时，EF∥AB？
（2）设四边形ABFE的面积为S（cm2），求S与t之间的函数关系式；
（3）当t为何值时，四边形ABFE的面积S等于矩形ABCD面积的38？
（4）当t为 103或5021103或5021时，△EFD是等腰三角形．
3
8
10
3
50
21
10
3
50
21
【考点】四边形综合题．
【答案】或
10
3
50
21
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/19 8:0:9组卷：371引用：3难度：0.4
相似题
-
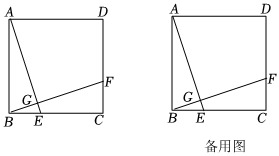1．如图，正方形ABCD中，点E，F分别在BC，CD上，BE=CF，AE，BF交于点G．
（1）求∠AGF的度数；
（2）在线段AG上截取MG=BG，连接DM，∠AGF的角平分线交DM于点N．
①依题意补全图形；
②用等式表示线段MN与ND的数量关系，并证明．发布：2025/5/22 14:0:1组卷：1952引用：3难度：0.3 -
2．（1）问题提出
如图1，在直角△ABC中，∠ACB=90°，AC=6，BC=8，D为边AB上的一个动点，连接CD，则CD的最小长度为 ．
（2）问题探究
如图2，在矩形ABCD中，四边形EFGH为矩形的内接四边形，点E，F，G，H分别在AD，AB，BC，CD上．FH为对角线，且满足FH∥AD，若AD=6，AB=4，则四边形EFGH的面积是否为定值？若是，求出该定值；若不是，请说明理由．
（3）问题解决
如图3，某果蔬基地规划修建一片试验区，并将试验区划分为四个区域．按照设计图的思路，试验区的平面示意图为四边形ABCD，∠ADC=90°，点O在四边形ABCD的对角线AC上，且满足OD=50m,CD=110m,OB∥AD，∠OBC=30°，设BO=x m,．S△ABC=ym2
①请写出y关于x的函数关系式；
②由于果蔬基地占地有限，探究y是否存在最小值．若存在，求出y值；若不存在，请说明理由．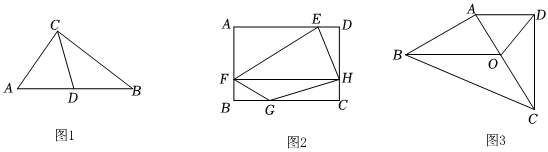
发布：2025/5/22 14:0:1组卷：268引用：2难度：0.1 -
3．问题提出
（1）如图1，在△ABC中，点D在BC上，连接AD，CD=2BD，则△ABD与△ACD的面积之比为 ；
问题探究
（2）如图2，在矩形ABCD中，AB=4，BC=8，点P为矩形内一动点，在点P运动的过程中始终有∠APB=45°，求△APB面积的最大值；（结果保留根号）
问题解决
（3）如图3，某市欲规划一块形如平行四边形ABCD的休闲旅游观光区，点A为观光区的入口，并满足∠BAD=120°，要求在边BC上确定一点E为观光区的南门，为了方便市民游览，修建一条观光通道AE（观光通道的宽度不计），且BE=2CE，AE=300米，为了容纳尽可能多的游客，要求平行四边形ABCD的面积最大，请问是否存在满足上述条件的面积最大的平行四边形ABCD？若存在，求出平行四边形ABCD的最大面积；若不存在，请说明理由．（结果保留根号）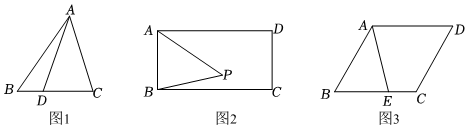
发布：2025/5/22 14:0:1组卷：735引用：4难度：0.1
