2021-2022学年四川省成都市树德中学高一（下）段考数学试卷（5月份）

一、选择题（本题共12小题，每小题5分，共60分，在每小题四个选项中只有一项是符合题目要求的）

• 1．在等比数列{a_n}中，a₇=9，则log₃a₅+log₃a₉=（　　）

  A．2

  B．3

  C．4

  D．9
  组卷：15引用：1难度：0.8

  解析

• 2．在△ABC中，若B=120°，C=15°，a=2，则此三角形的最大边长为（　　）

  A． 2 2

  B． 6

  C． 2 3

  D． 3 2
  组卷：2引用：1难度：0.7

  解析

• 3．将函数y=sin2x+

  3

  cos

  2

  x

  的图象沿x轴向左平移φ（φ＞0）个单位后，得到关于y轴对称的图象，则φ的最小值为（　　）

  A． π 12

  B． π 6

  C． π 4

  D． 5 π 12
  组卷：256引用：5难度：0.8

  解析

• 4．如图（1）、（2）、（3）、（4）是四个几何体的三视图，这四个几何体依次分别是（　　）

  A．三棱台、三棱柱、圆锥、圆台

  B．三棱台、三棱锥、圆锥、圆台

  C．三棱柱、四棱锥、圆锥、圆台

  D．三棱柱、三棱台、圆锥、圆台
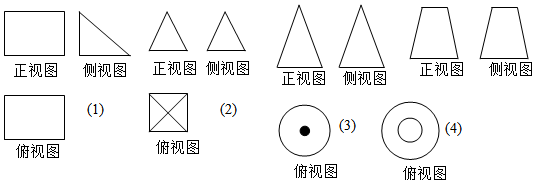  组卷：46引用：4难度：0.9

  解析

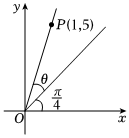• 5．已知锐角θ的大小如图所示，则sin2θ=（　　）

  A． 2 3

  B． 5 13

  C． 12 13

  D． - 12 13
  组卷：6引用：1难度：0.7

  解析

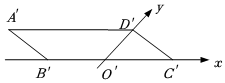• 6．把四边形ABCD按斜二测画法得到平行四边形A'B'C'D'（如图所示），其中B'O'=O'C'=2，O'D'=

  3

  ，则四边形ABCD一定是一个（　　）

  A．菱形

  B．矩形

  C．正方形

  D．梯形
  组卷：437引用：5难度：0.6

  解析

• 7．设D为△ABC所在平面内一点，

  AD

  =-

  1

  3

  AB

  +

  4

  3

  AC

  ，若

  BC

  =λ

  DC

  （λ∈R），则λ=（　　）

  A．2

  B．3

  C．-2

  D．-3
  组卷：3434引用：13难度：0.5

  解析

三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）

• 21．如图，在△ABC中，AC⊥BC．延长BA到D，使得AD=2，且∠CDA=

  π

  6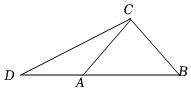

  ．
  （1）若AC=

  2

  ，求△DBC的面积；
  （2）当AC＜AD时，求△ACD面积的取值范围．
  组卷：246引用：4难度：0.6

  解析

• 22．已知数列{b_n}中，b₁=1，（b_n+1-1）•（b_n+3）=-4．正项等比数列{a_n}的公比q∈N^*，且满足（a₁-1）•a₃=8，a₁+

  a

  2

  2

  =18．
  （1）证明数列

  {

  1

  b

  n

  +

  1

  }

  为等差数列，并求数列{a_n}和{b_n}的通项公式；
  （2）如果c_n=

  a

  n

  +

  1

  •

  b

  n

  +

  1

  n

  ，求{c_n}的前n项和为T_n；
  （3）若存在n∈N^*，使（b₁+3）•（b₂+3）•（b₃+3）⋯（b_n+3）≤kn²成立，求实数k的取值范围．
  组卷：17引用：1难度：0.5

  解析