2023-2024学年河南省南阳一中高二(上)开学数学试卷
发布:2024/8/10 0:21:48
一、单选题(共8个小题,每小题5分,共40分.)
-
1.已知i为虚数单位,若复数
,则z=4-i22-i=( )z组卷:77引用:5难度:0.8 -
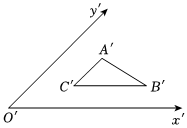 2.如图所示是利用斜二测画法画出的水平放置的△ABC的直观图,已知A′C′∥y′轴,B′C′∥x′轴且2A′C′=B′C′=2,则△ABC的周长为( )组卷:136引用:5难度:0.7
2.如图所示是利用斜二测画法画出的水平放置的△ABC的直观图,已知A′C′∥y′轴,B′C′∥x′轴且2A′C′=B′C′=2,则△ABC的周长为( )组卷:136引用:5难度:0.7 -
3.已知非零向量
,a满足b=(b,1),<3,a>=b,若(π3-a)⊥b,则向量a在向量a方向上的投影向量为( )b组卷:532引用:7难度:0.7 -
4.在平面直角坐标系xOy中,已知△ABC的顶点A(-4,0)和C(4,0),顶点B在椭圆
上,则x225+y29=1等于( )sinA+sinCsinB组卷:173引用:12难度:0.7 -
5.经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)两点的线段总有公共点,则直线l的倾斜角的取值范围是( )
组卷:493引用:5难度:0.7 -
6.下列直线中,与圆x2+y2=4相切的有( )
组卷:86引用:1难度:0.8 -
7.过点P(1,2)引一条直线,使它与点A(2,3)和点B(4,-5)的距离相等,那么这条直线的方程是( )
组卷:345引用:10难度:0.9
四、解答题(共6个小题,共70分.)
-
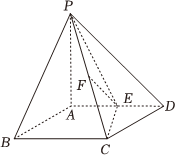 21.四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,∠ADC=60°,PA=AD=2,E为AD的中点,F为PC中点.
21.四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,∠ADC=60°,PA=AD=2,E为AD的中点,F为PC中点.
(1)求证:EF∥平面PAB;
(2)求PC与平面PAD所成的角的正切值;
(3)求二面角A-PD-C的正弦值.组卷:152引用:3难度:0.5 -
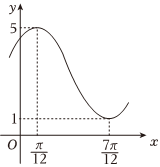 22.已知函数的部分图象如图所示.f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π2)
22.已知函数的部分图象如图所示.f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π2)
(1)求函数f(x)的解析式;
(2)将函数y=f(x)图象上所有的点向右平移个单位长度,再将所得图象上每一个点的横坐标变为原来的2倍(纵坐标不变),得到函数y=g(x)的图象.当π4时,方程g(x)-a=0恰有三个不相等的实数根,x1,x2,x3(x1<x2<x3),求实数a的取值范围以及x1+2x2+x3的值.x∈[0,13π6]组卷:326引用:7难度:0.6


