2022-2023学年湖南省常德市八年级（下）期中数学试卷

一、选择题(本大题共8个小题,每小题3分,满分24分

• 1．下列图形中是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：3引用：1难度：0.9

  解析

• 2．在一个直角三角形中，有一个锐角等于35°，则另一个锐角的度数是（　　）

  A．145°

  B．125°

  C．65°

  D．55°
  组卷：378引用：6难度：0.5

  解析

• 3．如图，在▱ABCD中，若∠B+∠D=100°，则∠B的度数为（　　）

  A．50°

  B．65°

  C．100°

  D．130°
  组卷：18引用：2难度：0.7

  解析

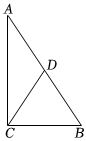• 4．如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，若AB=8，则CD的长是（　　）

  A．8

  B．6

  C．4

  D．2
  组卷：73引用：3难度：0.6

  解析

• 5．在下列条件中，不能判定四边形为平行四边形的是（　　）

  A．对角线互相平分

  B．一组对边平行且相等

  C．两组对边分别平行

  D．一组对边平行，另一组对边相等
  组卷：664引用：13难度：0.5

  解析

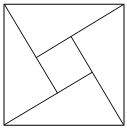• 6．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a,较短直角边长为b,若（a+b）²=21，大正方形的面积为13，则小正方形的面积为（　　）

  A．6

  B．5

  C．8

  D．7
  组卷：612引用：6难度：0.5

  解析

• 7．下列说法正确的是（　　）

  A．平行四边形的对角线互相平分且相等

  B．正方形的对角线相等且互相垂直平分

  C．对角线互相垂直的四边形是菱形

  D．对角线相等的四边形是矩形
  组卷：127引用：5难度：0.5

  解析

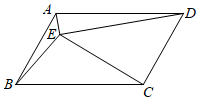• 8．如图，在平行四边形ABCD中，AB=2，点E为平行四边形内一点且∠AED=∠BEC=90°，若∠DEC=45°，则AD的长为（　　）

  A．3

  B．2 2

  C． 5 2

  D．2 3
  组卷：2841引用：5难度：0.3

  解析

七、(本题共2个小题,每小题10分,共20分

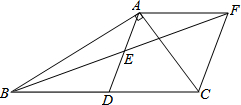• 25．如图，在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
  （1）求证：四边形ADCF是菱形；
  （2）若AC=7，AB=24，求菱形ADCF的面积．
  组卷：690引用：5难度：0.6

  解析

• 26．在等腰Rt△ABC中，∠BAC=90°，以C为底角顶点作等腰Rt△CED，使∠CED=90°，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
  （1）如图1，当点E在AC边上（不与点A、C重合），且D在△ABC外部时，求证：△AEF是等腰直角三角形；
  （2）如图2，将图1中△CED绕点C逆时针旋转，当点E落在线段BC上时，连接AE，求证：AF=

  2

  AE；
  （3）如图3，将△CED绕点C继续逆时针旋转，当平行四边形ABFD为菱形，且△CED在△ABC的下方时，若AB=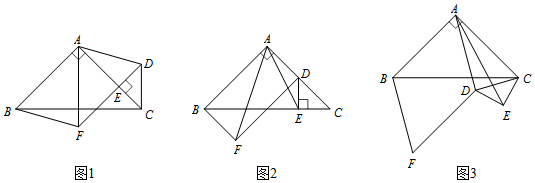

  15

  ，CE=

  6

  ，求线段AE的长．
  
  组卷：439引用：3难度：0.3

  解析