2023年浙江省金华市兰溪市中考数学调研试卷（4月份）
发布：2024/6/30 8:0:9
一、选择题。(本题共有10小题，每小题3分，共30分）
-
1．-2023的相反数是（ ）
组卷：3613引用：387难度：0.9 -
2．兰溪游埠是一座有着一千三百多年历史的古镇，与乌镇，南浔，佛堂并称为浙江四镇，游埠早茶更有“江南第一早茶”的美誉．2023年春节期间游埠古镇累计接待约3游客，其中33万用科学记数法表示为（ ）
组卷：12引用：1难度：0.8 -
3．下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（ ）
组卷：556引用：13难度：0.8 -
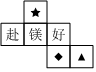4．2023年3月18日起，兰溪进入“镁”时间．一个正方体的表面分别标有共、赴、镁、好、之、约，如图是该正方体的表面展开图，已知“镁”的对面为“约”，则（ ）组卷：77引用：1难度：0.7 -
5．若
=x2，则y5=（ ）2x+yx组卷：367引用：3难度：0.7 -
6．如果关于x的一元二次方程ax2+bx+1=0的一个解是x=1，则代数式2023-a-b的值为（ ）
组卷：830引用：4难度：0.5 -
7．“直角”在几何学习中无处不在，如图图中的∠AOB一定是直角的是（ ）
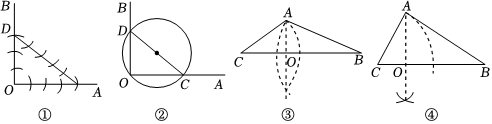组卷：104引用：1难度：0.7 -
8．习近平总书记指出，中华优秀传统文化是中华民族的“根”和“魂”．为了大力弘扬中华优秀传统文化，某校决定开展名著阅读活动．用3600元购买“四大名著”若干套后，发现这批图书满足不了学生的阅读需求，图书管理员在购买第二批时正赶上图书城八折销售该套书，于是用2400元购买的套数只比第一批少4套．设第一批购买的“四大名著”每套的价格为x元，则符合题意的方程是（ ）
组卷：1134引用：16难度：0.6
三、解答题。(本题有8小题，共66分,各小题都必须写出解答过程)
-
23．项目化学习：车轮的形状
[问题提出]车轮为什么要做成圆形，这里面有什么原理？
[合作探究]
（1）探究A组：如图1，圆形车轮半径为6cm,其车轮轴心O到地面的距离始终为 cm；
（2）探究B组：如图2，正方形车轮的轴心为O，若正方形的边长为6cm,求车轮轴心O距离地面的最高点与最低点的高度差；
（3）探究C组：如图3，有一个破损的圆形车轮，半径为6cm,破损部分是一个弓形，其所对圆心角为 90°，车轮轴心为O，让车轮在地上无滑动地滚动一周，求点O经过的路程．
（探究发现：车辆的平稳关键看车轮轴心是否稳定，即车轮轴心是否在一条水平线上运动．）
[拓展延伸]如图4，分别以正三角形的三个顶点A，B，C为圆心，以正三角形的边长为半径作60°圆弧，这样形成的曲线图形叫做“莱洛三角形”．
（4）探究D组：使“莱洛三角形”沿水平方向向右滚动．在滚动过程中，其“最高点”“车轮轴心O”均在不断移动位置，那么在“莱洛三角形”滚动的过程中，其“最高点“和“车轮轴心O”所形成路径的大致图案是 ．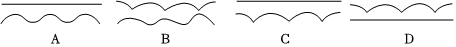
（延伸发现：“莱洛三角形”在滚动时始终位于一组平行线之间，因此放在其上的物体也能够保持平衡，但其车轴中心O并不稳定．）组卷：316引用：2难度：0.2 -
24．如图1，Rt△ABC中，∠B=90°，AB=3，BC=4，沿直线AC翻折△ABC得到△AB'C．如图2，延长BC和AB′，点E从点A的位置沿射线AB′方向平移，且作DE∥AC，DF∥CB′．同时动点P和Q出发，点P从点A沿线段AC向终点C运动，点Q从点D沿线段DE向终点E运动．设运动时间为t,点E平移的速度为每秒
个单位．53
（1）问点P和点Q平移的速度分别为多少时，才能使四边形EPCQ始终成为矩形；
（2）在（1）的条件下，
①问t为何值时，矩形EPCQ是正方形；
②t为何值时，矩形EPCQ面积最大，并求出最大面积．
（3）在（1）的条件下，当直线PQ经过四边形ABDF其中一个顶点时，求t的值．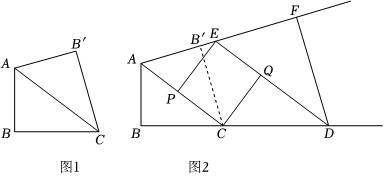
组卷：49引用：1难度：0.1
