项目化学习：车轮的形状
[问题提出]车轮为什么要做成圆形，这里面有什么原理？
[合作探究]
（1）探究A组：如图1，圆形车轮半径为6cm,其车轮轴心O到地面的距离始终为 66cm；
（2）探究B组：如图2，正方形车轮的轴心为O，若正方形的边长为6cm,求车轮轴心O距离地面的最高点与最低点的高度差；
（3）探究C组：如图3，有一个破损的圆形车轮，半径为6cm,破损部分是一个弓形，其所对圆心角为 90°，车轮轴心为O，让车轮在地上无滑动地滚动一周，求点O经过的路程．
（探究发现：车辆的平稳关键看车轮轴心是否稳定，即车轮轴心是否在一条水平线上运动．）
[拓展延伸]如图4，分别以正三角形的三个顶点A，B，C为圆心，以正三角形的边长为半径作60°圆弧，这样形成的曲线图形叫做“莱洛三角形”．
（4）探究D组：使“莱洛三角形”沿水平方向向右滚动．在滚动过程中，其“最高点”“车轮轴心O”均在不断移动位置，那么在“莱洛三角形”滚动的过程中，其“最高点“和“车轮轴心O”所形成路径的大致图案是 AA．
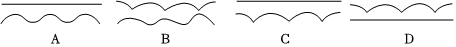
（延伸发现：“莱洛三角形”在滚动时始终位于一组平行线之间，因此放在其上的物体也能够保持平衡，但其车轴中心O并不稳定．）
【考点】圆的综合题．
【答案】6；A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：317引用：2难度：0.2
相似题
-
1．对于平面直角坐标系xOy中的线段PQ，给出如下定义：若存在△PQR使得S△PQR=PQ2，则称△PQR为线段PQ的“等幂三角形”，点R称为线段PQ的“等幂点”．
（1）已知A（3，0）．
①在点P1（1，3），P2（2，6），P3（-5，1），P4（3，-6）中，是线段OA的“等幂点”的是；
②若存在等腰△OAB是线段OA的“等幂三角形”，求点B的坐标；
（2）已知点C的坐标为C（2，-1），点D在直线y=x-3上，记图形M为以点T（1，0）为圆心，2为半径的⊙T位于x轴上方的部分．若图形M上存在点E，使得线段CD的“等幂三角形”△CDE为锐角三角形，直接写出点D的横坐标xD的取值范围．发布：2025/5/23 10:0:1组卷：821引用：2难度：0.5 -
2．A，B是⊙C上的两个点，点P在⊙C的内部．若∠APB为直角，则称∠APB为AB关于⊙C的内直角，特别地，当圆心C在∠APB边（含顶点）上时，称∠APB为AB关于⊙C的最佳内直角．如图1，∠AMB是AB关于⊙C的内直角，∠ANB是AB关于⊙C的最佳内直角．在平面直角坐标系xOy中．
（1）如图2，⊙O的半径为5，A（0，-5），B（4，3）是⊙O上两点．
①已知P1（1，0），P2（0，3），P3（-2，1），在∠AP1B，∠AP2B，∠AP3B中，是AB关于⊙O的内直角的是 ；
②若在直线y=2x+b上存在一点P，使得∠APB是AB关于⊙O的内直角，求b的取值范围．
（2）点E是以T（t,0）为圆心，4为半径的圆上一个动点，⊙T与x轴交于点D（点D在点T的右边）．现有点M（1，0），N（0，n），对于线段MN上每一点H，都存在点T，使∠DHE是DE关于⊙T的最佳内直角，请直接写出n的最大值，以及n取得最大值时t的取值范围．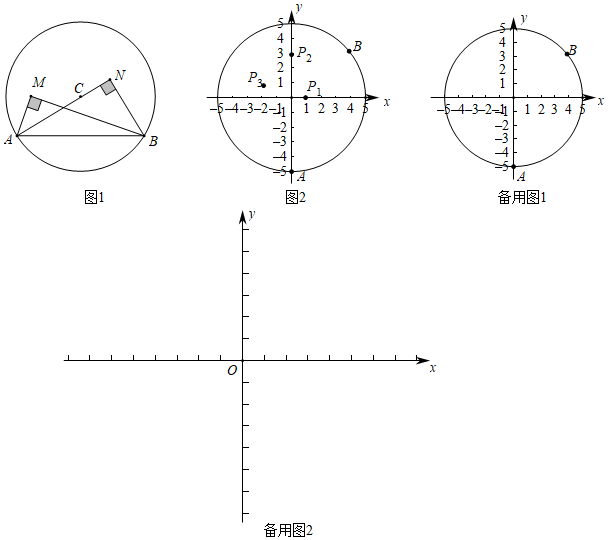
发布：2025/5/23 9:30:1组卷：1662引用：10难度：0.1 -
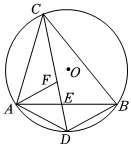3．已知：⊙O内接△ABC，CD平分∠ACB交AB于点E，交⊙O于点D，AF平分∠BAC交CD于点F，连接AD，BD．
（1）求证：AD=BD；
（2）求证：∠DAF=∠AFD；
（3）若点E为DF中点，BD=2，求CF长？发布：2025/5/23 10:0:1组卷：130引用：1难度：0.5
