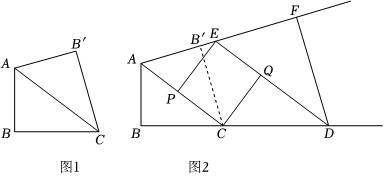
如图1，Rt△ABC中，∠B=90°，AB=3，BC=4，沿直线AC翻折△ABC得到△AB'C．如图2，延长BC和AB′，点E从点A的位置沿射线AB′方向平移，且作DE∥AC，DF∥CB′．同时动点P和Q出发，点P从点A沿线段AC向终点C运动，点Q从点D沿线段DE向终点E运动．设运动时间为t,点E平移的速度为每秒53个单位．
（1）问点P和点Q平移的速度分别为多少时，才能使四边形EPCQ始终成为矩形；
（2）在（1）的条件下，
①问t为何值时，矩形EPCQ是正方形；
②t为何值时，矩形EPCQ面积最大，并求出最大面积．
（3）在（1）的条件下，当直线PQ经过四边形ABDF其中一个顶点时，求t的值．
5
3
【考点】四边形综合题．
【答案】（1）点P的速度是每秒1个单位，点Q速度是每秒个单位；
（2）①；
②当t=时，S矩形EPCQ最大=；
（3）=3或时，直线PQ经过四边形ABDF其中一个顶点．
16
9
（2）①
15
7
②当t=
5
2
25
3
（3）=3或
45
13
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：49引用：1难度：0.1
相似题
-
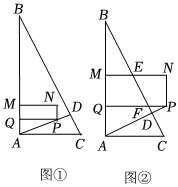1．如图①，在△ABC中，∠BAC=90°，AC=4，AB=8，AD⊥BC，动点P从点A出发，沿射线AD以每秒个单位长度的速度运动，过点P作AB的垂线交AB于点Q，以PQ为边向上作矩形PQMN，点M在AB或AB的延长线上，PQ=2QM，当点Q与点B重合时点P停止运动，设点P运动的时间为t（秒）．5
（1）求BC的长；
（2）当BC平分矩形PQMN的周长时，求t的值；
（3）当点N在△ABC的直角边的垂直平分线上时，直接写出t的值；
（4）如图②，当点P在AD的延长线上时，MN、PQ分别交边BC于点E、F，当△PFD与图中某个三角形全等时，求t的值．发布：2025/5/23 10:30:1组卷：100引用：1难度：0.2 -
2．如图1，在平行四边形ABCD中，AC与BD交于点O，EF∥BD，且EF交AC于点M．
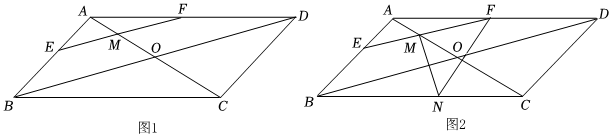
（1）求证：EM=FM；
（2）如图2，过点M作MN⊥EF交BC于点N，连接NF，若∠BNM=2∠EFN，∠FNC=50°，∠ADC=45°，FN=8．
①求BN的长；
②若，求AE=32．S△AEMS四边形MODF发布：2025/5/23 11:0:1组卷：117引用：1难度：0.5 -
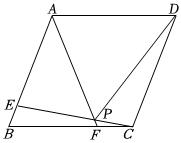3．已知菱形ABCD中，∠BAD=120°，点E、F分别在AB、BC上，BE=CF，AF与CE交于点P．
（1）求证：∠APE=60°；
（2）当PC=1，PA=5时，求PD的长；
（3）当AB=2时，求PD的最大值．3发布：2025/5/23 9:30:1组卷：176引用：3难度：0.5
