2022-2023学年湖南省株洲市炎陵县高二（下）期末数学试卷

一、单选题（本大题共8个小题，每小题5分，共40分）

• 1．已知集合A={x|4x＜1}，B={x|-3＜6x＜8}，则A∪B=（　　）

  A． { x | x ＜ 1 4 }

  B． { x | - 1 2 ＜ x ＜ 1 4 }

  C． { x | x ＜ 4 3 }

  D． { x | - 1 2 ＜ x ＜ 3 4 }
  组卷：162引用：5难度：0.8

  解析

• 2．若复数

  z

  =

  2

  1

  +

  i

  ，则|z+2-3i|=（　　）

  A． 13

  B． 17

  C．4

  D．5
  组卷：86引用：2难度：0.9

  解析

• 3．若正实数a、b满足a+2b=1，则当ab取最大值时，a的值是（　　）

  A． 1 2

  B． 1 4

  C． 1 6

  D． 1 8
  组卷：683引用：5难度：0.7

  解析

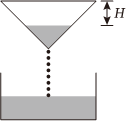• 4．如图所示，液体从一个圆锥形漏斗漏入一个圆柱形桶中，开始时漏斗中盛满液体，经过3秒漏完，圆柱形桶中液面上升速度是一个常量，则漏斗中液面下降的高度H与下降时间t之间的函数关系的图象只可能是（　　）

  A．

  B．

  C．

  D．
  组卷：20引用：2难度：0.7

  解析

• 5．已知函数f（x）满足f（2^x）=log₂x,则f（16）=（　　）

  A．-1

  B．1

  C．2

  D．4
  组卷：50引用：5难度：0.8

  解析

• 6．已知向量

  m

  =（sinωx,

  3

  2

  ），

  n

  =（

  1

  2

  ，cosωx）（ω＞0），设函数f（x）=

  m

  •

  n

  ，若x=

  5

  π

  6

  为f（x）图象的对称轴，（

  π

  3

  ，0）为f（x）图象的对称中心，且f（x）在区间（

  π

  12

  ，

  π

  6

  ）上单调，则ω的值为（　　）

  A．5

  B．7

  C．9

  D．11
  组卷：71引用：3难度：0.5

  解析

• 7．已知α，β是两个不同的平面，m,n是两条不同的直线，则下列正确的结论是（　　）

  A．若m∥n,m∥α，n∥β，则α∥β	B．若α∥β，m⊂α，n⊂β，则m∥n
  C．若m⊥n,m⊥α，n⊥β，则α⊥β	D．若m⊥n,m⊥α，n∥β，则α⊥β
  组卷：96引用：6难度：0.7

  解析

四、解答题（本大题共6个小题，共70分。解答应写出文字说明、证明过程或演算步骤）

• 21．已知某电子公司生产某款手机的年固定成本为40万美元，每生产1万部还需另投入16万美元，设该公司一年内共生产该款手机x万部并全部销售完，每万部的销售收入为R（x）万美元，且R（x）=

  400 - 6 x , 0 ≤ x ≤ 40

  7400 x - 40000 x 2 ， x ＞ 40

  ．
  （1）写出年利润W（万美元）关于年产量x（万部）的函数解析式（利润=销售收入-成本）；
  （2）当年产量为多少万部时，该公司在该款手机的生产中所获得的利润最大？并求出最大利润．
  组卷：127引用：11难度：0.6

  解析

• 22．已知函数f（x）=log₂（4^x+1）+kx为偶函数．
  （1）求实数k的值；
  （2）解关于m的不等式f（2m+1）＞f（m-1）；
  （3）设g（x）=log₂（a•2^x+a）（a≠0），若函数h（x）=f（x）-g（x）有2个零点，求实数a的取值范围．
  组卷：225引用：3难度：0.4

  解析