当前位置：试卷中心 > 试卷详情

2023-2024学年广东省广州市荔湾区真光中学高三（上）月考数学试卷（9月份）

发布：2024/8/29 0:0:8

一、单选题

1．若集合A={1，2，3}，集合B={z|z=x-y,x∈A，y∈A}，则集合A∪B=（　　）
A．{1，2} B．{1，2，3}
C．{-2，-1，0，1，2} D．{-2，-1，0，1，2，3}
组卷：98引用：4难度：0.8
解析
2．设复数
z
=
2
+
i
i
+
i
2
+
i
4
，则
z
=（　　）
A．1-2i B．1+2i C．2-i D．2+i
组卷：30引用：3难度：0.8
解析
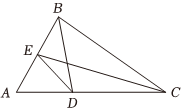3．如图所示的△ABC中，点D是线段AC上靠近A的三等分点，点E是线段AB的中点，则
DE
=（　　）
A．-
1
3
BA
-
1
6
BC
B．-
5
6
BA
-
1
3
BC
C．-
1
6
BA
-
1
3
BC
D．-
5
6
BA
+
1
3
BC
组卷：199引用：10难度：0.7
解析
4．已知α，λ∈R，则“sinα=λcosα”是“tanα=λ”的（　　）
A．充分不必要条件 B．充要条件
C．必要不充分条件 D．既不充分也不必要条件
组卷：79引用：2难度：0.8
解析
5．设某芯片制造厂有甲、乙两条生产线均生产5nm规格的芯片，现有20块该规格的芯片，其中甲、乙生产的芯片分别为12块，8块，且乙生产该芯片的次品率为
1
20
，现从这20块芯片中任取一块芯片，若取得芯片的次品率为0.08，则甲厂生产该芯片的次品率为（　　）
A．
1
5
B．
1
10
C．
1
15
D．
1
20
组卷：63引用：7难度：0.7
解析
6．直线l经过椭圆的两个顶点，若椭圆中心到l的距离为其长轴长的
1
6
，则该椭圆的离心率为（　　）
A．
2
3
B．
3
5
C．
6
4
D．
14
4
组卷：213引用：4难度：0.7
解析
7．已知数列{a_n}满足a₁=1，且a_n+1=a_n+2，数列{b_n}满足b₁=1，b_n+1-b_n=a_n+1，则
b
n
+
8
n
的最小值为（　　）
A．
13
3
B．5 C．
4
2
D．
17
3
组卷：301引用：7难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题

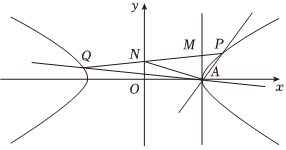21．已知双曲线
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
，渐近线方程为
y
±
x
2
=
0
，点A（2，0）在C上；
（1）求双曲线C的方程；
（2）过点A的两条直线AP，AQ分别与双曲线C交于P，Q两点（不与A点重合），且两条直线的斜率k₁，k₂满足k₁+k₂=1，直线PQ与直线x=2，y轴分别交于M，N两点，求证：△AMN的面积为定值．
组卷：128引用：4难度：0.5
解析
22．在三维空间中，立方体的坐标可用三维坐标（a₁，a₂，a₃）表示，其中a_i∈{0，1}（1≤i≤3，i∈N）．而在n维空间中（n≥2，n∈N），以单位长度为边长的“立方体”的顶点坐标可表示为n维坐标（a₁，a₂，a₃，⋯⋯，a_n），其中a_i∈{0，1}（1≤i≤n,i∈N）．现有如下定义：在n维空间中两点间的曼哈顿距离为两点（a₁，a₂，a₃，⋯⋯，a_n）与（b₁，b₂，b₃，⋯⋯，b_n）坐标差的绝对值之和，即为|a₁-b₁|+|a₂-b₂|+|a₃-b₃|+⋯⋯+|a_n-b_n|．回答下列问题：
（1）求出n维“立方体”的顶点数；
（2）在n维“立方体”中任取两个不同顶点，记随机变量X为所取两点间的曼哈顿距离
①求出X的分布列与期望；
②证明：在n足够大时，随机变量X的方差小于0.25n²．
（已知对于正态分布X～N（μ，σ²），P随X变化关系可表示为
φ
μ
，
σ
（
x
）
=
1
σ
2
π
•
e
-
（
x
-
μ
）
2
2
σ
2
）
组卷：292引用：7难度：0.4
解析