2022-2023学年浙江省丽水市高二（下）期末数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={-1，0，1，2}，B={x|0＜x＜3}，则A∩B=（　　）

  A．{-1，0，1}

  B．{0，1}

  C．{-1，1，2}

  D．{1，2}
  组卷：2572引用：43难度：0.9

  解析

• 2．在△ABC中，角A，B，C所对的边分别为a,b,c,已知a=4，

  b

  =

  4

  3

  ，B=60°，则角A=（　　）

  A．30°

  B．45°

  C．30°或150°

  D．45°或135°
  组卷：72引用：3难度：0.7

  解析

• 3．“2^a＞2^b”是“

  1

  a

  ＜

  1

  b

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：87引用：6难度：0.9

  解析

• 4．在平面直角坐标系中，角α的顶点在坐标原点，始边与x轴的非负半轴重合，角α的终边与圆心在坐标原点的单位圆交于点

  P

  （

  -

  4

  5

  ，

  3

  5

  ）

  ，则cos2α=（　　）

  A． - 24 25

  B． 24 25

  C． - 7 25

  D． 7 25
  组卷：70引用：2难度：0.8

  解析

• 5．已知函数f（2x+1）是奇函数，f（x+2）是偶函数，当x∈[2，3]时，f（x）=3-x,则下列选项不正确的是（　　）

  A．f（x）在区间（-2，0）上单调递减

  B．f（x）的图象关于直线x=-1对称

  C．f（x）的最大值是1

  D．当x∈（-1，1）时恒有f（x）＜0
  组卷：239引用：2难度：0.2

  解析

• 6．已知△OAB中，OA=2，OB=1，

  OA

  •

  OB

  =

  -

  1

  ，过点O作OD垂直AB于点D，则（　　）

  A． OD = 5 7 OA + 2 7 OB	B． OD = 2 7 OA + 5 7 OB
  C． OD = 4 7 OA + 3 7 OB	D． OD = 3 7 OA + 4 7 OB
  组卷：32引用：2难度：0.7

  解析

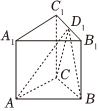• 7．如图，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，AA₁=2，AC=BC=1，∠ACB=90°，D在上底面A₁B₁C₁（包括边界）上运动，则三棱锥D-ABC的外接球体积的最大值为（　　）

  A． 6 2 π

  B． 3 π

  C． 6 π

  D． 3 3 2 π
  组卷：41引用：2难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

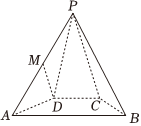• 21．在四棱锥P-ABCD中，△PAB为正三角形，四边形ABCD为等腰梯形，M为棱AP的中点，且AB=2AD=2BC=2CD=4，

  DM

  =

  3

  ．
  （1）求证：平面PDC⊥平面ABCD；
  （2）求平面PAD与平面PBC所成锐二面角的余弦值．
  组卷：49引用：2难度：0.4

  解析

• 22．已知函数f（x）=-|x²-2|-ax.
  （Ⅰ）当a=1时，求f（x）的零点；
  （Ⅱ）若关于x的方程f（x）+2x²+2=0区间（0，4]上有三个不同的解x₁，x₂，x₃，且x₁＜x₂＜x₃，求x₁x₂x₃的取值范围；
  （Ⅲ）当a＞0时，若在[0，2]上存在2023个不同的实数x_i（i=1，2，…，2023），x₁＜x₂＜…＜x₂₀₂₃，使得|f（x₁）-f（x₂）|+|f（x₂）-f（x₃）|+…+|f（x₂₀₂₂）-f（x₂₀₂₃）|=6，
  求实数a的取值范围．
  组卷：40引用：1难度：0.5

  解析