当前位置：试卷中心 > 试卷详情

2023-2024学年陕西省西安市新城区五环中学八年级（上）第一次月考数学试卷

发布：2024/9/21 0:0:8

一、选择题（共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的）

1．要使
x
-
2
有意义，则x的值可以是（　　）
A．0 B．-1 C．-2 D．2
组卷：854引用：12难度：0.8
解析
2．下列各组数中，是勾股数的是（　　）
A．0.3，0.4，0.5 B．3，4，5
C．
3
，
4
，
5
D．5，7，12
组卷：116引用：3难度：0.7
解析
3．下列二次根式中，是最简二次根式的是（　　）
A．
32
B．
90
C．
3
2
D．
5
组卷：130引用：6难度：0.7
解析
4．下列运算正确的是（　　）
A．
3
+
6
=
9
B．
3
5
-
5
=
2
C．
24
÷
6
=
4
D．
3
×
5
=
15
组卷：150引用：7难度：0.6
解析
5．下列说法中，错误的是（　　）
A．8的立方根是±2
B．4的算术平方根是2
C．
81
的平方根是±3
D．立方根等于-1的实数是-1
组卷：1823引用：13难度：0.7
解析
6．如图，一支铅笔放在圆柱体笔筒中，笔筒的内部底面直径是9cm,内壁高12cm,则这支铅笔的长度可能是（　　）
A．9cm B．12cm C．15cm D．18cm
组卷：1685引用：20难度：0.7
解析
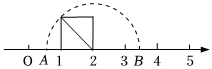7．如图，以数轴的单位长度线段为边作一个正方形，以表示数2的点为圆心，正方形对角线长为半径画半圆，交数轴于点A和点B，则点A表示的数是（　　）

A．
2
+
2
B．
2
-
2
C．
2
D．
1
-
2
组卷：1094引用：9难度：0.8
解析
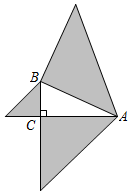8．如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形．若
AB
=
3
，则图中阴影部分的面积为（　　）
A．3 B．
9
2
C．
3
2
D．
3
5
组卷：1942引用：14难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共13小题，计81分.解答应写出过程）

25．我们之前学习有理数时，知道两个数的乘积为1则这两个数互为倒数．在学习二次根式的过程中，小明研究发现有一些特殊的无理数之间具有互为倒数的关系．例如：由
（
2
+
1
）
（
2
-
1
）
=
1
，可得
2
+
1
与
2
-
1
互为倒数，即
1
2
+
1
=
2
-
1
或
1
2
-
1
=
2
+
1
，类似地，
（
3
+
2
）
（
3
-
2
）
=
1
，可得
1
3
+
2
=
3
-
2
或
1
3
-
2
=
3
+
2
．
根据小明发现的规律，解决下列问题：
（1）
1
7
+
6
=
，
1
n
+
1
+
n
=
（n为正整数）；
（2）若
1
2
3
+
a
=
2
3
-
a
，则a=
；
（3）求
1
2
+
1
+
1
3
+
2
+
1
4
+
3
+
…
+
1
100
+
99
的值．
组卷：139引用：4难度：0.6
解析
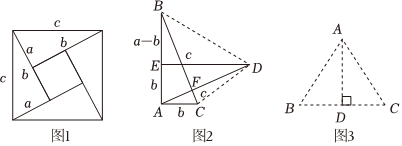26．【背景介绍】勾股定理是几何学中的明珠，充满着魅力．如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理，思路是大正方形的面积有两种求法，一种是等于c²另一种是等于四个直角三角形与一个小正方形的面积之和，即
1
2
ab
×
4
+
（
b
-
a
）
2
从而得到等式
c
2
=
1
2
ab
×
4
+
（
b
-
a
）
2
化简使得结论a²+b²=c²这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双求法”．
【方法运用】千百年来，人们对勾股定理的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向常春在2010年构造发现了一个新的证法：把两个全等的Rt△ABC和Rt△DEA如图2放置，其三边长分别为a,b,c,∠BAC=∠DEA=90°显然BC⊥AD．
（1）请用a,b,c分别表示出四边形ABDC，梯形AEDC，△EBD的面积，再探究这三个图形面积之间的关系，证明勾股定理a²+b²=c²；
【方法迁移】
（2）如图3，在△ABC中，AD是BC边上的高，AB=4，AC=5，BC=6，设BD=x,求x的值．
组卷：504引用：2难度：0.5
解析