2022-2023学年陕西省铜川市宜君高级中学高一(下)期中数学试卷
发布:2024/5/23 8:0:8
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1.已知向量
,a=(1,-3),则b=(3,12)=( )a+2b组卷:219引用:4难度:0.8 -
2.若复数z满足z-i=1-
i,则z在复平面内所对应的点位于( )12组卷:48引用:3难度:0.8 -
3.已知正三角形ABC的边长为2,那么△ABC的直观图△A′B′C′的面积为( )
组卷:562引用:10难度:0.7 -
4.已知向量
=2(cosα,sinα),|a|=b,且(3+a)•b=7,则a与a的夹角为( )b组卷:65引用:3难度:0.7 -
5.如图所示,用符号语言可表达为( )
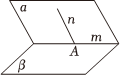 组卷:327引用:13难度:0.5
组卷:327引用:13难度:0.5 -
6.设a,b是两条不同的直线,α,β是两个不同的平面,则下列选项正确的为( )
组卷:42引用:1难度:0.6 -
7.△ABC的内角A,B,C的对边分别为a,b,c.若(sinB+sinC)2-sin2(B+C)=3sinBsinC,且a=2,则△ABC的面积的最大值是( )
组卷:697引用:8难度:0.6
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
 21.如图所示,在四棱锥P-ABCD中,BC∥平面PAD,BC=AD,E是PD的中点.12
21.如图所示,在四棱锥P-ABCD中,BC∥平面PAD,BC=AD,E是PD的中点.12
(Ⅰ)求证:BC∥AD;
(Ⅱ)求证:CE∥平面PAB;
(Ⅲ)若M是线段CE上一动点,则线段AD上是否存在点N,使MN∥平面PAB?说明理由.组卷:4040引用:20难度:0.6 -
22.已知①a=2,
,②B=π4在这三个条件中任选两个,补充在下面的问题中,并解决该问题.③c=23b
在△ABC中,角A,B,C的对边分别为a,b,c,且满足.(b-a)(sinB+sinA)=c(3sinB-sinC)
(1)求角A的大小;
(2)已知_____,_____,若△ABC存在,求△ABC的面积;若不存在,说明理由.组卷:223引用:8难度:0.5


