2023-2024学年江苏省南京市秦淮中学、溧水二高等四校高二（上）第一次学情调研数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分.

• 1．抛物线y=4x²的焦点坐标是（　　）

  A．（0，1）

  B．（1，0）

  C． （ 0 ， 1 16 ）

  D． （ 1 16 ， 0 ）
  组卷：606引用：175难度：0.9

  解析

• 2．已知点A（2，1），点B在直线x-y+3=0上，则|AB|的最小值为（　　）

  A． 5

  B． 26

  C．2 2

  D．4
  组卷：336引用：14难度：0.8

  解析

• 3．双曲线C：

  x

  2

  a

  2

  -

  y

  2

  5

  =

  1

  （

  a

  ＞

  4

  3

  ）

  的右顶点为A，点A到直线

  x

  =

  4

  3

  距离为

  2

  3

  ，则C的离心率为（　　）

  A． 6 2

  B． 3 5 5

  C． 3 2

  D． 5 2
  组卷：118引用：3难度：0.7

  解析

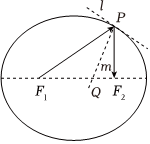• 4．班级物理社团在做光学实验时，发现了一个有趣的现象：从椭圆的一个焦点发出的光线经椭圆形的反射面反射后将汇聚到另一个焦点处．根据椭圆的光学性质解决下面问题：已知椭圆C的方程为

  x

  2

  16

  +

  y

  2

  12

  =1，其左、右焦点分别是F₁，F₂，直线l与椭圆C切于点P，且PF₁=5，过点P且与直线l垂直的直线m与椭圆长轴交于点Q，则

  F

  1

  Q

  F

  2

  Q

  =（　　）

  A． 5 2

  B． 15 3

  C． 5 4

  D． 5 3
  组卷：30引用：4难度：0.7

  解析

• 5．直线xsinα+y+2=0的倾斜角的取值范围是（　　）

  A．[0，π）	B．[0， π 4 ]∪[ 3 π 4 ，π）
  C．[0， π 4 ]	D．[0， π 4 ]∪（ π 2 ，π）
  组卷：4009引用：75难度：0.9

  解析

• 6．已知圆C：x²+（y-a）²=8（a∈R）和两点A（2，0），B（0，2），若圆C上存在四个不同的点P，使得△ABP的面积为2，则a的取值范围是（　　）

  A．（-4，0）

  B．（0，4）

  C．（-4，4）

  D．（-4，8）
  组卷：33引用：4难度：0.5

  解析

• 7．已知圆C的半径为1，圆心在直线l：y=x+3上．点A（-1，0），B（1，0）．若圆C上存在点P，使得PA²+PB²=10，则圆心C的横坐标a的取值范围为（　　）

  A．[-3，-2]

  B．[-3，0]

  C．[-2，-1]

  D．[-1，0]
  组卷：167引用：2难度：0.6

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.

• 21．平面直角坐标系xOy中，过椭圆M：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）右焦点的直线x+y-

  3

  =0交M于A，B两点，且椭圆M的离心率为

  2

  2

  ．
  （1）求椭圆M的方程；
  （2）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．
  组卷：108引用：3难度：0.5

  解析

• 22．已知一动圆Q与圆M：（x+1）²+y²=1外切，同时与圆N：（x-1）²+y²=25内切，圆心Q的轨迹为曲线C．
  （1）求曲线C的方程；
  （2）过曲线C上点P作该曲线的一条切线l与直线x=1相交于点A，与直线x=9相交于点B，证明PN⊥NB并判断

  |

  AN

  |

  |

  BN

  |

  是否为定值？若是，求出该值；若不是，请说明理由．
  组卷：91引用：4难度：0.5

  解析