2022-2023学年浙江省台州市山海协作体高一（下）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求．

• 1．若a,b∈R，i是虚数单位，且b+（a-2）i=1+i,则a+b的值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：53引用：10难度：0.9

  解析

• 2．已知向量

  a

  =（4，2），向量

  b

  =（x,3），且

  a

  ∥

  b

  ，则x=（　　）

  A．9

  B．6

  C．5

  D．3
  组卷：558引用：28难度：0.9

  解析

• 3．已知圆锥的底面半径为1，高为

  2

  2

  ，则圆锥的侧面积为（　　）

  A．6π

  B．3π

  C． 3 2 π

  D．π
  组卷：251引用：5难度：0.8

  解析

• 4．在△ABC中，已知a=4，b=4

  3

  ，B=60°，则角A的度数为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：252引用：12难度：0.9

  解析

• 5．已知非零向量

  a

  ，

  b

  满足|

  a

  |=2|

  b

  |，且（

  a

  -

  b

  ）⊥

  b

  ，则

  a

  与

  b

  的夹角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：14731引用：122难度：0.5

  解析

• 6．设非零向量

  a

  ，

  b

  的夹角为150°，且

  |

  a

  |

  =

  |

  a

  +

  b

  |

  ，则

  |

  2

  a

  +

  t

  b

  |

  |

  b

  |

  的最小值是（　　）

  A． 3 3

  B． 3 6

  C． 3

  D． 2 3
  组卷：67引用：1难度：0.6

  解析

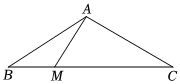• 7．如图，在△ABC中，M为BC边上一点，

  BC

  =

  4

  BM

  ，∠AMC=60°，AM=2，△ABC的面积为

  4

  3

  ，则cos∠BAC等于（　　）

  A． 1 2

  B． 21 7

  C． - 21 7

  D． - 1 2
  组卷：125引用：1难度：0.5

  解析

四、解答题：本⼤题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

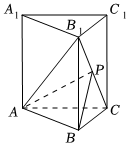• 21．如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90，且AC=BC=CC₁=2，点P为线段B₁C上的动点．
  （Ⅰ）当P为线段B₁C中点时，求证平面ABP⊥平面AB₁C；
  （Ⅱ）当直线AP与平面BCC₁B₁所成角的正切值为

  3

  2

  2

  时，求二面角P-AB-C的余弦值．
  组卷：187引用：4难度：0.5

  解析

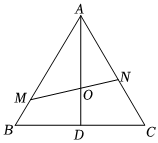• 22．如图，在边长为1的正三角形ABC中，D为BC的中点，

  AO

  =

  2

  OD

  ，过点O的直线交边AB与点M，交边AC于点N．
  （Ⅰ）用

  AB

  ，

  AC

  表示

  AO

  ；
  （Ⅱ）若

  AM

  =

  m

  AB

  ，

  AN

  =

  n

  AC

  ，求

  1

  m

  +

  1

  n

  的值；
  （Ⅲ）求OM²+ON²的取值范围．
  组卷：132引用：2难度：0.4

  解析