2022-2023学年湖南省岳阳市岳阳楼区八年级（下）期末数学试卷
发布：2024/6/22 8:0:10
一、选择题（本大题共10道小题，每小题3分，满分30分，在每道小题给出的四个选项中，选出符合要求的一项）
-
1．在平面直角坐标系中，点（-1，3）所在的象限是（ ）
组卷：294引用：14难度：0.9 -
2．下列图案中是中心对称图形的是（ ）
组卷：58引用：4难度：0.9 -
3．对某班学生在家做家务的时间进行调查后，将所得数据分成4组，第一组的频率为0.15，第二组和第三组的频率之和为0.75，则第四组的频率为（ ）
组卷：123引用：5难度：0.8 -
4．在函数y=2x-3中，当自变量x=5时，函数值等于（ ）
组卷：417引用：7难度：0.8 -
5．若一个多边形的内角和为540°，则这个多边形是（ ）
组卷：350引用：31难度：0.9 -
6．下列有关一次函数y=-4x-2的说法中，正确的是（ ）
组卷：2025引用：11难度：0.7 -
7．下列命题中，不正确的是（ ）
组卷：20引用：2难度：0.5 -
8．图1是第七届国际数学教育大会（ICME）会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形OABC．若AB=BC=2，且∠AOB=30°，则OC的长度为（ ）组卷：534引用：15难度：0.7
三、解答题（本大题共9个小题，共72分，解答应写出文字说明、证明过程或演算步骤）
-
24．“先天下之忧而忧，后天下之乐而乐”这是《岳阳楼记》中的一句千古名言，也是岳阳精神的真实写照，这句话具有鲜明的对称美．如果一个凸四边形沿着它的一条对角线对折后能完全重合，我们就把这个四边形称为“忧乐四边形”．如图1，凸四边形ABCD沿对角线AC对折后完全重合，四边形ABCD是以直线AC为对称轴的“忧乐四边形”．
（1）下列四边形一定是“忧乐四边形”的有 （填序号）；
①平行四边形②长方形③正方形④菱形⑤梯形
（2）在四边形ABCD中，点E是BC边上的中点，四边形ABEF是以直线AE为对称轴的“忧乐四边形”（点F在四边形ABCD内部），连接AF并延长交DC于点G．
①如图2，若四边形ABCD是矩形，求证：四边形FECG是“忧乐四边形”．
②如图3，若四边形ABCD是平行四边形，①中的结论是否仍然成立，请说明理由．
（3）如图4，四边形ABCD是正方形，且点E为线段BC上的动点（不与B、C重合），四边形ABEF是以直线AE为对称轴的“忧乐四边形”（点F在正方形ABCD内部），连接DF并延长，与AE的延长线交于点H，连接CH，请直接写出DH，AH，CH三条线段之间的数量关系．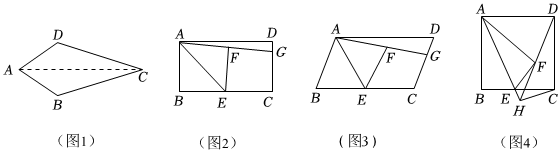
组卷：297引用：2难度：0.3 -
25．如图1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，直线DE经过点C，过A作AD⊥DE于点D．过B作BE⊥DE于点E，则△BEC≌△CDA，这是我们熟悉的一线三直角模型，我们称这种全等模型为“k字型全等”．
若一次函数y=kx+4（k≠0）的图象与x轴、y轴分别交于A、B两点．
（1）如图2，当k=-1时，若点B到经过原点的直线l的距离BE的长为3，求点A到直线l的距离AD的长；
（2）如图3，当k=-时，点M在第一象限内，若△ABM是以AB为斜边的等腰直角三角形，求点M的坐标；43
（3）我们知道：随着k值的变化，点A的位置也会变化．若k＞0，如图4，将线段BA绕点B逆时针旋转90°后得到线段BA′．
①当B、O、A′三点构成等腰三角形时，求点A′的坐标及k的值．
②若△BOA′是钝角三角形，请直接写出k的取值范围．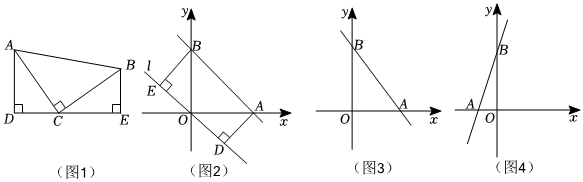
组卷：269引用：1难度：0.1
