2023-2024学年北京市丰台区高一（上）期中数学试卷（A卷）

一、选择题：本部分共10小题，每小题4分，共40分.在每小题给出的四个选项中，选出最符合题意的一项.

• 1．已知集合A={x∈Z|x＜3}，则（　　）

  A．2∈A

  B．3∈A

  C．0∉A

  D．∅∈A
  组卷：205引用：3难度：0.9

  解析

• 2．命题“∀x≥2，x²≥4”的否定为（　　）

  A．“∀x≤2，x2≥4”	B．“ ∃ x 0 ＜ 2 ， x 2 0 ＜ 4 ”
  C．“∀x≥2，x2＜4”	D．“ ∃ x 0 ≥ 2 ， x 2 0 ＜ 4 ”
  组卷：111引用：4难度：0.9

  解析

• 3．下列函数中，既是偶函数又在（0，+∞）上单调递增的是（　　）

  A．y=-|x|

  B．y=x2

  C．y=x3

  D． y = - 1 x
  组卷：78引用：6难度：0.5

  解析

• 4．下列说法正确的是（　　）

  A．若a＞b,则ac2＞bc2	B．若a＞b,则a-1＜b-2
  C．若 a c 2 ＞ b c 2 ，则a＞b	D．若a＞b,则a2＞b2
  组卷：239引用：8难度：0.7

  解析

• 5．已知幂函数y=f（x）的图象经过点

  （

  2

  ，

  2

  ）

  ，则f（4）等于（　　）

  A．2

  B．-2

  C． 2

  D．4
  组卷：132引用：1难度：0.7

  解析

• 6．设x∈R，则“2-x≥0”是“|x+1|≤1”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：858引用：10难度：0.8

  解析

• 7．设M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列四个图形：
  
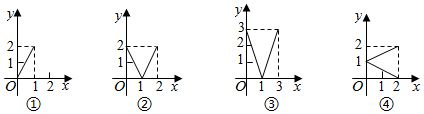
  其中，能表示从集合M到集合N的函数关系的个数是（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：737引用：13难度：0.9

  解析

三、解答题：本题共6小题，共85分，解答应写出文字说明，演算步骤或证明过程.

• 20．某企业开发、生产了一款新型节能环保产品，对市场需求调研后，决定提高产品的产量，投入90万元安装了一台新设备，并立即进行生产，预计使用该设备前n年（n∈N^*）的材料费、维修费、人工工资等共

  （

  5

  2

  n

  2

  +

  5

  n

  ）

  万元，每年的销售收入为55万元，设使用该设备前n年的总盈利额为f（n）万元．
  （Ⅰ）写出f（n）关于n的函数关系式，并计算该设备从第几年开始使企业盈利；
  （Ⅱ）使用若干年后，对该设备的处理方案有两种：
  方案一：当总盈利额达到最大值时，该设备以10万元的价格处理；
  方案二：当年平均盈利额达到最大值时，该设备以50万元的价格处理．
  问选择哪种处理方案更合适？请说明理由．
  组卷：57引用：6难度：0.5

  解析

• 21．对于函数f（x），若f（x₀）=x₀，则称x₀为f（x）的“不动点”；若f[f（x₀）]=x₀，则称x₀为f（x）的“稳定点”．函数f（x）的“不动点”和“稳定点”的集合分别记为A和B，即A={x|f（x）=x}，B={x|f[f（x）]=x}．
  （1）设函数f（x）=3x+4，求集合A和B；
  （2）求证：A⊆B；
  （3）设函数f（x）=ax²+bx+c（a≠0），且A=∅，求证：B=∅．
  组卷：533引用：12难度：0.1

  解析