当前位置：试卷中心 > 试卷详情

2022-2023学年重庆市北碚区西南大学附中九年级（上）月考数学试卷（12月份）

发布：2024/8/3 8:0:9

2．下列调查中，适宜采用普查方式的是（　　）

A．调查全国中学生心理健康现状

B．调查一片试验田里某种大麦的穗长情况

C．调查冷饮市场上冰淇淋的质量情况

D．调查你所在班级的每一个同学所穿鞋子的尺码情况

组卷：944引用：14难度：0.9

3．如图是由4个相同的小正方体组成的立体图形，它的主视图是（　　）
A． B． C． D．
组卷：443引用：13难度：0.9
解析
4．若y轴负半轴上的点P到x轴的距离为2，则点P的坐标为（　　）
A．（0，2） B．（2，0） C．（-2，0） D．（0，-2）
组卷：319引用：5难度：0.9
解析
5．为了了解某市参加中考的32000名学生的体重情况，抽查了其中1600名学生的体重进行统计分析．下列叙述正确的是（　　）
A．32000名学生是总体
B．1600名学生的体重是总体的一个样本
C．每名学生是总体的一个个体
D．样本容量是1600名
组卷：256引用：4难度：0.8
解析
6．已知点A（-1，1），B（5，1），点C在y轴上，且△ABC的面积为9，则点C的坐标为（　　）
A．（0，4） B．（0，4）或（0，-2）
C．（0，3） D．（4，0）或（-2，0）
组卷：147引用：6难度：0.5
解析
7．如果一组数据6，7，x,9，5的平均数是2x,那么这组数据的中位数为（　　）
A．5 B．6 C．7 D．9
组卷：610引用：8难度：0.8
解析
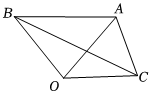8．如图，如果△ABC外一点O满足OA=OB=OC，∠OAB=45°，∠OBC=24°，那么∠OCA的大小是（　　）
A．65° B．24° C．69° D．45°
组卷：45引用：3难度：0.7
解析

25．如果一个自然数N的个位数字不为0，且能分解成A×B，其中A与B都是两位数，A的十位数字比B的十位数字大2，A、B的个位数字之和为10，则称数N为“美好数”，并把数N分解成N=A×B的过程，称为“美好分解”．例如：∵2989=61×49，61的十位数字比49的十位数字大2，且61、49的个位数字之和为10，∴2989是“美好数”；又如：∵605=35×19，35的十位数字比19的十位数字大2，但个位数字之和不等于10，∴605不是“美好数”．
（1）判断525，1148是否是“美好数”？并说明理由；
（2）把一个大于4000的四位“美好数”N进行“美好分解”，即分解成N=A×B，A的各个数位数字之和的2倍与B的各个数位数字之和的和能被7整除，求出所有满足条件的N．
组卷：182引用：2难度：0.6
解析
26．已知点D在△ABC外，∠BAC=90°，AB=AC，射线BD与△ABC的边AC交于点H，AE⊥BD，垂足为E，∠ABD=∠ACD．
（1）如图1，若∠ABE=30°，AH=4，求DH；
（2）求证：BE=DC+DE；
（3）如图2，若∠ABE=25°，BE=4，点F在线段BC上，且BE=BF，点M，N分别是射线BC、BD上的动点，在点M，N运动的过程中，请判断式子EM+MN+NF的值是否存在最小值，若存在，请求出这个最小值；若不存在，写出你的理由．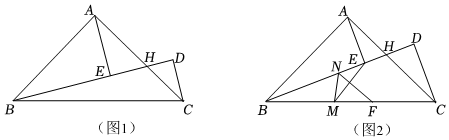
组卷：188引用：2难度：0.2
解析