2023-2024学年重庆市南开中学高一（上）开学数学试卷

一、单选题（本题共8小题，每小题5分，共40分．在每小题给出的选项中，只有一项符合题目要求）

• 1．设全集U=R，A={-2，-1，0，1，2}，B={x|x≤-1或x＞2}，则（∁_UB）∩A=（　　）

  A．{0，1}

  B．{-1，0}

  C．{0，1，2}

  D．{-1，0，1}
  组卷：109引用：7难度：0.9

  解析

• 2．若集合A={-1，1}，B={x|mx=2}，且B⊆A，则实数m的值（　　）

  A．-2

  B．2

  C．2或-2

  D．2或-2或0
  组卷：310引用：11难度：0.7

  解析

• 3．关于x的一元二次方程mx²-3x+1=0有实数根，则实数m的取值范围是（　　）

  A． m ≤ 9 4 且m≠0

  B． m ≥ 9 4

  C． m ＜ 9 4 且m≠0

  D． m ≤ 9 4
  组卷：66引用：1难度：0.7

  解析

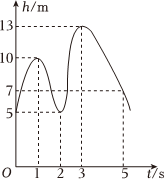• 4．如图，曲线表示一只蝴蝶在飞行过程中离地面的高度h（m）随行时间t（s）的变化情况，则这只蝴蝶飞行的最高高度约为（　　）

  A．5m

  B．7m

  C．10m

  D．13m
  组卷：9引用：1难度：0.8

  解析

• 5．用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（　　）
  

  A．32

  B．34

  C．37

  D．41
  组卷：29引用：1难度：0.8

  解析

• 6．估计

  3

  ×

  （

  2

  3

  +

  5

  ）

  的值应在（　　）

  A．10和11之间

  B．9和10之间

  C．8和9之间

  D．7和8之间
  组卷：30引用：1难度：0.8

  解析

• 7．有三支股票A，B，C，28位股民的持有情况如下：每位股民至少持有其中一支股票．在不持有A股票的人中，持有B股票的人数是持有C股票的人数的2倍．在持有A股票的人中，只持有A股票的人数比除了持有A股票外，同时还持有其它股票的人数多1．在只持有一支股票的人中，有一半持有A股票．则只持有B股票的股民人数是（　　）

  A．7

  B．6

  C．5

  D．4
  组卷：355引用：5难度：0.7

  解析

四、解答题（本大题共70分，解答应写出文字说明，证明过程或演算步骤，所有作答过程都写在答题卡相对应位置上）

• 21．若一个四位数M的个位数字与十位数字的平方和恰好是M去掉个位与十位数字后得到的两位数，则这个四位数M为“勾股和数”．
  例如：M=2543，∵3²+4²=25，∴2543是“勾股和数”；
  又如：M=4325，∵5²+2²=29，29≠43，∴4325不是“勾股和数”．
  （1）判断2022，5055是否是“勾股和数”，并说明理由；
  （2）一个“勾股和数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记G（M）=

  c

  +

  d

  9

  ，P（M）=

  |

  10

  （

  a

  -

  c

  ）

  +

  （

  b

  -

  d

  ）

  |

  3

  ．当G（M），P（M）均是整数时，求出所有满足条件的M．
  组卷：13引用：1难度：0.7

  解析

• 22．设集合A为n元数集，若A的2个非空子集B，C满足：B∪C=A，B∩C=∅，则称B，C为A的一个二阶划分．记B中所有元素之和为S（B），C中所有元素之和为S（C）．
  （Ⅰ）若A={1，2，3}，求A的一个二阶划分，使得S（B）=2S（C）；
  （Ⅱ）若A={1，2，⋯，10}．求证：不存在A的二阶划分B，C满足S（C）=2S（B）；
  （Ⅲ）若A={1，2，⋯，n}（n≥3，n∈N^*），B，C为A的一个二阶划分，满足：①若x∈B，则2x∉B；②若x∈C，则2x∉C．
  记f（n）为符合条件的B的个数，求f（n）的解析式．
  组卷：153引用：3难度：0.5

  解析