2022-2023学年福建省安溪一中、养正中学、惠安一中、泉州实验中学高二（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的

• 1．集合A={x|0≤x＜4，且x∈N}的真子集的个数是（　　）

  A．16

  B．8

  C．15

  D．4
  组卷：263引用：4难度：0.7

  解析

• 2．已知a∈R，则（a+1）（a-2）＜0是0＜a＜1成立的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：722引用：8难度：0.7

  解析

• 3．实数a,b满足a≥b,则下列不等式成立的是（　　）

  A． a b ≥ 1

  B．tana≥tanb

  C．2a-b≥1

  D．ln（a-b）≥0
  组卷：190引用：7难度：0.7

  解析

• 4．在平行六面体ABCD-A₁B₁C₁D₁中，M为A₁C₁与B₁D₁的交点，若

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则与

  BM

  相等的向量是（　　）

  A． 1 2 a + 1 2 b + c

  B． - 1 2 a - 1 2 b + c

  C． 1 2 a - 1 2 b + c

  D． - 1 2 a + 1 2 b + c
  组卷：419引用：3难度：0.7

  解析

• 5．已知圆（x-1）²+（y+2）²=1关于直线2ax-by-2=0（a＞0，b＞0）对称，则ab的最大值为（　　）

  A．2

  B．1

  C． 1 2

  D． 1 4
  组卷：151引用：1难度：0.5

  解析

• 6．设F为抛物线

  C

  1

  ：

  y

  2

  =

  2

  x

  的焦点，点P在抛物线上，点Q在准线l上，满足PQ∥x轴．若|PQ|=|QF|，则|PF|=（　　）

  A．2

  B． 2 3

  C．3

  D． 3 3
  组卷：146引用：6难度：0.7

  解析

• 7．已知由样本数据点集合{x_i=y_i）|i=1，2，⋯，n}，求得的回归直线方程l₁为

  ̂

  y

  =1.5x+0.5，且

  x

  =3．现发现两个数据点（1.3，2.1）和（4.7，7.9）误差较大，去除这两点后重新求得的回归直线方程l₂的斜率为1.2，则正确的是（　　）

  A．变量x与y具有负相关关系

  B．去除后y的估计值增加速度变快

  C．去除后回归方程为y=1.2x+1.6

  D．去除后相应于样本点（2，3.75）的残差为-0.05
  组卷：25引用：1难度：0.6

  解析

四．解答题：本题共6题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知函数f（x）=xlnx-kx.
  （1）求f（x）的单调区间；
  （2）若对任意的x∈（2，+∞），k∈Z，不等式f（x）+2k+1＞0恒成立，求整数k的最大值．
  组卷：168引用：2难度：0.2

  解析

• 22．已知双曲线C：

  x

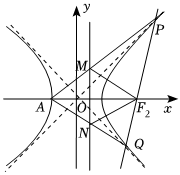  2

  -

  y

  2

  b

  2

  =

  1

  （

  b

  ＞

  0

  ）

  的左、右焦点分别为F₁，F₂，A是C的左顶点，C的离心率为2．设过F₂的直线l交C的右支于P、Q两点，其中P在第一象限．
  （1）求C的标准方程；
  （2）若直线AP、AQ分别交直线

  x

  =

  1

  2

  于M、N两点，证明：

  M

  F

  2

  •

  N

  F

  2

  为定值；
  （3）是否存在常数λ，使得∠PF₂A=λ∠PAF₂恒成立？若存在，求出λ的值；否则，说明理由．
  组卷：135引用：3难度：0.5

  解析