当前位置：试卷中心 > 试卷详情

2023-2024学年广东省六校联考高一（上）期中数学试卷

发布：2024/9/25 7:0:2

一．单选题（本题共8小题，每小题5分，共40分）

1．已知集合M={-1，1，2}，N={x∈R|x²=x}，则M∪N=（　　）
A．{1} B．{-1，0} C．{-1，0，1，2} D．{-1，0，2}
组卷：212引用：12难度：0.7
解析
2．若非零实数a,b满足|a|＞|b|，则下列不等式中一定成立的是（　　）
A．a-b＞0 B．a²-b²＞0 C．a³-b³＞0 D．
1
a
＜
1
b
组卷：171引用：8难度：0.7
解析
3．已知函数y=f（x）的定义域为[-2，3]，则函数
y
=
f
（
2
x
+
1
）
x
+
1
的定义域为（　　）
A．
[
-
3
2
，
1
]
B．
[
-
3
2
，-
1
）
∪
（
-
1
，
1
]
C．[-3，7] D．[-3，-1）∪（-1，7]
组卷：1924引用：20难度：0.8
解析
4．设f（x）是定义域为R的奇函数，且f（1+x）=f（-x）．若f（-
1
3
）=
1
3
，则f（
5
3
）=（　　）
A．-
5
3
B．-
1
3
C．
1
3
D．
5
3
组卷：7413引用：46难度：0.7
解析
5．已知函数y=（2m-1）x^m+n-2是幂函数，一次函数y=kx+b（k＞0，b＞0）的图象过点（m,n），则
4
k
+
1
b
的最小值是（　　）
A．3 B．
9
2
C．
14
3
D．5
组卷：360引用：8难度：0.7
解析
6．“
a
∈
（
-
1
3
，
3
]
”是“函数f（x）=
x
2
-
（
a
-
1
）
x
+
2
，
x
≥
1
（
3
a
+
1
）
x
-
5
，
x
＜
1
是定义在R上的增函数”的（　　）
A．必要不充分条件 B．充分不必要条件
C．充分必要条件 D．既不充分也不必要条件
组卷：254引用：6难度：0.6
解析
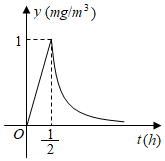7．新型冠状病毒导致的疫情还没有完全解除．为了做好校园防疫工作，某学校决定每天对教室进行消毒．已知消毒药物在释放过程中，室内空气中的含药量y（单位：mg/m³）与时间t（单位：小时）成正比
（
0
＜
t
＜
1
2
）
．药物释放完毕后，y与t的函数关系式为
y
=
（
1
4
）
t
-
a
（a为常数，
t
≥
1
2
）．按照规定，当空气中每立方米的含药量降低到0.5mg/m³以下时，学生方可进入教室．因此，每天进行消毒的工作人员应当提前多长时间进行教室消毒？（　　）
A．30分钟 B．60分钟 C．90分钟 D．120分钟
组卷：190引用：5难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题

21．已知函数f（x）=x²-x,g（x）=2x-2．
（1）若∀x₁∈[0，3]，∃x₂∈[0，3]使得f（x₁）+m≤g（x₂）成立，求实数m的取值范围；
（2）当a≠0时，解关于x的不等式af（x）＞g（x）．
组卷：70引用：4难度：0.5
解析
22．定义在R上的奇函数f（x）=
x
,-
1
＜
x
＜
0
，
-
a
-
x
，
x
≤
-
1
，
其中a＞0，a≠1，且f（1）=e,其中e是自然对数的底数，e=2.71828⋯．
（1）当x≥0时，求函数f（x）的解析式；
（2）若存在x₂＞x₁≥0，满足f（x₂）=ef（x₁），求x₁•f（x₂）的取值范围．
组卷：193引用：2难度：0.4
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． [ - 3 2 ， 1 ]	B． [ - 3 2 ，- 1 ） ∪ （ - 1 ， 1 ]
C．[-3，7]	D．[-3，-1）∪（-1，7]

A．必要不充分条件	B．充分不必要条件
C．充分必要条件	D．既不充分也不必要条件

2023-2024学年广东省六校联考高一（上）期中数学试卷

一．单选题（本题共8小题，每小题5分，共40分）

1．已知集合M={-1，1，2}，N={x∈R|x2=x}，则M∪N=（ ）

2．若非零实数a,b满足|a|＞|b|，则下列不等式中一定成立的是（ ）

3．已知函数y=f（x）的定义域为[-2，3]，则函数y=f（2x+1）x+1的定义域为（ ）

4．设f（x）是定义域为R的奇函数，且f（1+x）=f（-x）．若f（-13）=13，则f（53）=（ ）

5．已知函数y=（2m-1）xm+n-2是幂函数，一次函数y=kx+b（k＞0，b＞0）的图象过点（m,n），则4k+1b的最小值是（ ）

6．“a∈（-13，3]”是“函数f（x）=x2-（a-1）x+2，x≥1（3a+1）x-5，x＜1是定义在R上的增函数”的（ ）

四、解答题

21．已知函数f（x）=x2-x,g（x）=2x-2．（1）若∀x1∈[0，3]，∃x2∈[0，3]使得f（x1）+m≤g（x2）成立，求实数m的取值范围；（2）当a≠0时，解关于x的不等式af（x）＞g（x）．

1．已知集合M={-1，1，2}，N={x∈R|x²=x}，则M∪N=（　　）

2．若非零实数a,b满足|a|＞|b|，则下列不等式中一定成立的是（　　）

3．已知函数y=f（x）的定义域为[-2，3]，则函数
y
=
f
（
2
x
+
1
）
x
+
1
的定义域为（　　）

4．设f（x）是定义域为R的奇函数，且f（1+x）=f（-x）．若f（-
1
3
）=
1
3
，则f（
5
3
）=（　　）

5．已知函数y=（2m-1）x^m+n-2是幂函数，一次函数y=kx+b（k＞0，b＞0）的图象过点（m,n），则
4
k
+
1
b
的最小值是（　　）

6．“
a
∈
（
-
1
3
，
3
]
”是“函数f（x）=
x
2
-
（
a
-
1
）
x
+
2
，
x
≥
1
（
3
a
+
1
）
x
-
5
，
x
＜
1
是定义在R上的增函数”的（　　）

21．已知函数f（x）=x²-x,g（x）=2x-2．
（1）若∀x₁∈[0，3]，∃x₂∈[0，3]使得f（x₁）+m≤g（x₂）成立，求实数m的取值范围；
（2）当a≠0时，解关于x的不等式af（x）＞g（x）．