2022-2023学年江苏省扬州市江都区邵樊片九年级（下）第二次月考数学试卷
发布：2024/7/20 8:0:8
一、选择题（本题共8小题，每小题3分，共24分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选择项前的字母代号填涂在答题卡相应的位置上）
-
1．-3的倒数是（ ）
组卷：4983引用：687难度：0.9 -
2．在平面直角坐标系中，点A（-1，2）关于y轴对称的点B的坐标为（ ）
组卷：276引用：17难度：0.7 -
3．下列说法：
①一个游戏中奖的概率是，则做100次这样的游戏一定会中奖；1100
②为了了解全国中学生的心理健康状况，应采用普查的方式；
③为了疫情防控了解进校同学的体温状况，应采用抽样调查的方式；
④若甲组数据方差，乙组数据方差S2甲=0.2，则甲组数据比乙组数据稳定；S2乙=0.5
其中正确的有（ ）个．组卷：15引用：1难度：0.7 -
4．学校为了丰富学生课余活动开展了一次“爱我云南，唱我云南”的歌咏比赛，共有18名同学入围，他们的决赛成绩如下表：
则入围同学决赛成绩的中位数和众数分别是（ ）成绩（分） 9.40 9.50 9.60 9.70 9.80 9.90 人数 2 3 5 4 3 1 组卷：323引用：62难度：0.9 -
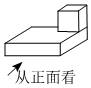5．如图，在一个长方体上放着一个小正方体，这个组合体的左视图是（ ）组卷：110引用：6难度：0.9 -
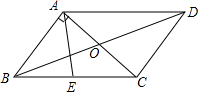6．如图，平行四边形ABCD的周长是26cm,对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多3cm,则AE的长度为（ ）组卷：7426引用：39难度：0.7 -
7．某公司上半年生产甲、乙两种型号的无人机若干架，已知甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架．设甲种型号无人机x架，乙种型号无人机y架，根据题意可列出的方程组是（ ）
组卷：1409引用：19难度：0.6 -
8．设P（x,y1），Q（x,y2）分别是函数C1，C2图象上的点，当a≤x≤b时，总有-1≤y1-y2≤1恒成立，则称函数C1，C2在a≤x≤b上是“逼近函数”，a≤x≤b为“逼近区间”．则下列结论：
①函数y=x-5，y=3x+2在1≤x≤2上是“逼近函数”；
②函数y=x-5，y=x2-4x在3≤x≤4上是“逼近函数”；
③0≤x≤1是函数y=x2-1，y=2x2-x的“逼近区间”；
④2≤x≤3是函数y=x-5，y=x2-4x的“逼近区间”．
其中，正确的有（ ）组卷：3154引用：7难度：0.4
二、填空题（本题共10个小题，每小题3分，共30分．不需写出解答过程，请把正确答案直接填写在答题卡相应位置上）
-
9．2023年扬州鉴真半程马拉松赛暨大运河马拉松系列赛（扬州站）于4月16日上午鸣枪开跑，来自世界各地的20000余名选手参加了这项国际赛事，将20000用科学记数法表示为 ．
组卷：17引用：1难度：0.8
三、解答题（本题共10个小题，共96分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
-
27．某企业生产并销售某种产品，假设销售量与产量相等，图中的线段AB表示该产品每千克生产成本y1（单位：元）与产量x（单位：kg）之间的函数关系；线段CD表示该产品销售价y2（单位：元）与产量x（单位：kg）之间的函数关系，已知0＜x≤120，m＞60．
（1）求线段AB所表示的y1与x之间的函数表达式；
（2）若m=90，该产品产量为多少时，获得的利润最大？最大利润是多少？
（3）若60＜m＜70，该产品产量为多少时，获得的利润最大？最大利润是多少？组卷：189引用：1难度：0.3 -
28．【问题情境】（1）点A是⊙O外一点，点P是⊙O上一动点．若⊙O的半径为2，且OA=5，则点P到点A的距离最长为 ．
【直接运用】（2）如图1，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于点D，P是弧CD上的一个动点，连接AP，则AP的最小值是 ．
【构造运用】（3）如图2，已知正方形ABCD的边长为6，点M、N分别从点B、C同时出发，以相同的速度沿逆时针方向向终点D和A运动，连接AM和BN交于点P，求tan∠DCP的最小值．
【灵活运用】（4）如图3，⊙O的直径为8，弦，点C为优弧AB上一动点，AM⊥AC交直线CB于点M，则△ABM的面积最大值是 ．AB=43
组卷：412引用：1难度：0.4
